Abstract
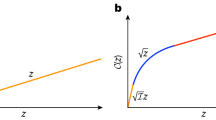
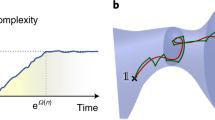
Differential geometry has long found applications in physics in general relativity and related areas. More recently, it was proposed by Nielsen that the tools of differential geometry, when applied to the unitary group, might be used to bound the complexity of quantum operations. The Bishop–Gromov bound—a cousin of the focusing lemmas used to prove the Penrose–Hawking black hole singularity theorems—is a differential geometry result that gives an upper bound on the rate of growth of the volume of geodesic balls in terms of the Ricci curvature. Here I apply the Bishop–Gromov bound to Nielsen’s complexity geometry to prove lower bounds on the quantum complexity of a typical unitary. For a broad class of models, the typical complexity is shown to be exponentially large in the number of qubits. This technique gives results that are tighter than all known lower bounds in the literature, as well as establishing lower bounds for a much broader class of complexity geometry metrics than has hitherto been bounded. This method thus realizes the original vision of Nielsen, which was to apply the tools of differential geometry to study quantum complexity.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout

Similar content being viewed by others
Data availability
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
References
Nielsen, M. A. A geometric approach to quantum circuit lower bounds. Preprint at arXiv:quant-ph/0502070
Nielsen, M. A., Dowling, M., Gu, M. & Doherty, A. C. Quantum computation as geometry. Science 311, 1133 (2006).
Nielsen, M. A., Dowling, M. R., Gu, M. & Doherty, A. C. Optimal control, geometry, and quantum computing. Phys. Rev. A 73, 062323 (2006).
Dowling, M. R. & Nielsen, M. A. The geometry of quantum computation. Preprint at arXiv:quant-ph/0701004
Gu, M., Doherty, A. & Nielsen, M. Quantum control via geometry: an explicit example. Phys. Rev. A 78, 032327 (2008).
Bishop, R. A relation between volume, mean curvature, and diameter. Not. Am. Math. Soc. 10, 364 (1963).
Nielsen, M. A. & Isaac, L. in Quantum Computation and Quantum Information Ch. 4 (Cambridge Univ. Press, 2010).
Brown, A. R. & Susskind, L. Complexity geometry of a single qubit. Phys. Rev. D 100, 046020 (2019).
Susskind, L. & Zhao, Y. Switchbacks and the bridge to nowhere. Preprint at arXiv:1408.2823 [hep-th].
Brown, A. R., Susskind, L. & Zhao, Y. Quantum complexity and negative curvature. Phys. Rev. D 95, 045010 (2017).
Balasubramanian, V., Decross, M., Kar, A. & Parrikar, O. Quantum complexity of time evolution with chaotic Hamiltonians. J. High Energy Phys. 2020, 134 (2020).
Auzzi, R. et al. Geometry of quantum complexity. Phys. Rev. D 103, 106021 (2021).
Balasubramanian, V., DeCross, M., Kar, A., Li, Y. & Parrikar, O. Complexity growth in integrable and chaotic models. J. High Energy Phys. 2021, 11 (2021).
Bulchandani, V. B. & Sondhi, S. L. How smooth is quantum complexity?. J. High Energy Phys. 2021, 30 (2021).
Wu, Q. F. Sectional curvatures distribution of complexity geometry. J. High Energy Phys. 2022, 197 (2022).
Basteiro, P. et al. Quantum complexity as hydrodynamics. Phys. Rev. D 106, 065016 (2022).
Jefferson, R. & Myers, R. C. Circuit complexity in quantum field theory. J. High Energy Phys. 10, 107 (2017).
Chapman, S., Heller, M. P., Marrochio, H. & Pastawski, F. Toward a definition of complexity for quantum field theory states. Phys. Rev. Lett. 120, 121602 (2018).
Khan, R., Krishnan, C. & Sharma, S. Circuit complexity in fermionic field theory. Phys. Rev. D 98, 126001 (2018).
Hackl, L. & Myers, R. C. Circuit complexity for free fermions. J. High Energy Phys. 2018, 139 (2018).
Raychaudhuri, A. Relativistic cosmology 1. Phys. Rev. 98, 1123–1126 (1955).
Milnor, J. Curvatures of left invariant metrics on lie groups. Adv. Math. 21, 93–329 (1976).
Susskind, L. Computational complexity and black hole horizons. Fortsch. Phys. 64, 24–43 (2016).
Stanford, D. & Susskind, L. Complexity and shock wave geometries. Phys. Rev. D 90, 126007 (2014).
Brown, A. R., Roberts, D. A., Susskind, L., Swingle, B. & Zhao, Y. Holographic complexity equals bulk action? Phys. Rev. Lett. 116, 191301 (2016).
Brown, A. R., Roberts, D. A., Susskind, L., Swingle, B. & Zhao, Y. Complexity, action, and black holes. Phys. Rev. D 93, 086006 (2016).
Brown, A. R. & Susskind, L. Second law of quantum complexity. Phys. Rev. D 97, 086015 (2018).
Brown, A. R., Freedman, M. H., Lin, H. W. & Susskind, L. Effective geometry, complexity, and universality. Preprint at arXiv:2111.12700 [hep-th].
Acknowledgements
I thank H. Lin, L. Susskind and, in particular, M. Freedman.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Peer review
Peer review information
Nature Physics thanks Michal Heller, Lucas Hackl and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary discussion and calculations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Brown, A.R. A quantum complexity lower bound from differential geometry. Nat. Phys. 19, 401–406 (2023). https://doi.org/10.1038/s41567-022-01884-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01884-6
This article is cited by
-
Universality in long-distance geometry and quantum complexity
Nature (2023)
-
Geometry and complexity scaling
Nature Physics (2023)
-
Is action complexity better for de Sitter space in Jackiw-Teitelboim gravity?
Journal of High Energy Physics (2023)