Introduction

Coeliac disease (CD) is a permanent immune-mediated intolerance to the gluten contained in cereals such as wheat, barley and rye. CD has a multigenic and multifactorial origin: the existence of a strong genetic predisposition is supported by a 10% prevalence in first-degree relatives and a 75% concordance in monozygotic twins, compared to 11% in dizygotic twins.1 A well-known predisposing factor lies in the HLA class II region. More than 85% of coeliac patients carry the same DQ heterodimer DQA1*05 DQB1*02 encoded in cis or in trans.2 Almost all the remaining cases carry either the DQA1*05 or the DQB1*02 part of the DQ heterodimer, or DRB1*04-DQ8. However, only part of the familial aggregation is explained by the HLA component, suggesting the presence of additional non-HLA genetic risk factors, as shown by the concordance rate of 20% in dizygotic twins sharing two HLA haplotypes identical by descent compared to 75% in monozygotic twins.1

The European Cluster on the Genetics of Coeliac Disease has been set up in 2000 to investigate the genetic component of CD. The collaboration involves six partners (Italy, Sweden, Norway, Finland, France and the UK). Within this cluster, four independent genome scans3,4,5,6 have been performed. While each study highlighted regions of interest, none of them achieved the genome-wide level of significance, except for the HLA region. Regions of interest were further investigated without definite conclusions,7,8,9,10 even if region 5q, originally found in the Italian genome scan7 gave repeatedly moderate evidence for linkage. The interpretation of regions that coincide is, however, not so easy to do. This study addresses the question by analysing the previous genome screens and follow-up studies within a common framework through two approaches: a meta-analysis and a mega-analysis, in which the individual data sets are pooled prior to analysis.

Many research groups across the world are studying the genetic component of the same human disease. The need for globally interpreting results has promoted the development of meta-analysis methods.11,12,13,14,15,16,17,18,19

The meta-analysis method used here is the Genome Screen Meta-Analysis (GSMA).13 The method is based on ranking genetic regions or bins according to the value of the statistic or of the P-value achieved in each scan. The first application of GSMA was on four published genome scans on multiple sclerosis. An extension of the method20 has been proposed to take into account studies performed on more restricted regions of the genome.

Since we had access to the raw data of each partner, it was possible to perform a pooled linkage analysis of the cluster data, or mega-analysis, in order to compare the results obtained by the two methods.

Family data

Families with a minimum of two affected siblings were collected in all participating countries as described in the individual papers. The affected individuals were almost exclusively diagnosed according to the ESPGHAN criteria.21 The Italian sample consists of 103 families from the genome-wide scan3 and 83 families from a replication study.7 The Scandinavian sample includes 60 families.5 Between 15 and 40 additional families, depending on the region, were used in the densification analysis.5,8 The Finnish sample totals 60 families for the full genome screen,6 and a second set of 38 families.9 The UK sample has 16 families in the genome-wide scan4 and an additional 34 families in the replication study.10 Some additional families and/or markers, not included in the original publications, were also made available to us.

All families are basically affected sibship families except for six of the initial 16 British families,4 which are more extended and one Finnish family with two affected sibships on three generations. When all the data are pooled together in a single data set, there are altogether 442 families with CD and raw genotypes of 2025 individuals of whom 1056 are affected. Parents were generally available except in the Finnish and British families. In total, 80% of all founders were available for genotyping.

Marker data

The marker and map panel used in the different screens were different from centre to centre, but the average intermarker distances were around 10–15 cM. All centres performed additional studies of more restricted regions. The number of regions and markers followed up also varied from centre to centre, with an intermarker spacing of the order of 5 cM.

Altogether 1092 markers, mostly microsatellites, were genotyped in at least one population. A common map of all markers was constructed using genetic distances from Marshfield (http://research.marshfieldclinic.org/genetics/). Markers that had the same position in Marshfield were ordered according to the human genome database (http://gdbwww.gdb.org) and arbitrarily separated by 0.01 cM. More than 97% of the markers were mapped in this way. When a marker was not found in the Marshfield database, other map databases were used and the genetic position interpolated using flanking markers available in both databases. Many markers were used in more than one population. Two problems had to be faced in these cases. The allele coding of the length polymorphisms was different and homogenous allele frequencies between populations could not a priori be assumed. Given the fact that 20% of founders are untyped, information on marker allele frequencies is needed to avoid potential bias in linkage analysis results. Both these problems can be nicely overcome by the same approach used in a meta-analysis of multiple sclerosis genome screens,22 that is, a prefix indicating the population was added to each marker name. So, for example, marker D1S2141 was called FD1S2141 when genotyped in Finnish families and SDS2141 when genotyped in Scandinavian families, but both synonyms have the same genetic position. The allele frequencies were separately estimated from the genotype data in each population.

Principle of meta-analysis by GSMA

To apply the GSMA method,13 the genome needs to be fragmented into bins of equal lengths. Based on the common map described above, each chromosome is divided into bins of approximately 30 cM, making sure that at least one marker from each country was present in any bin. This bin length was suggested by Wise et al as a good compromise to avoid having peaks corresponding to the same genetic risk factor falling into different bins and having peaks corresponding to two different genetic risk factors falling into the same bin. A total of 115 bins were thus available for ranking.

For each genome scan, the maximum value of the linkage statistic obtained in each bin scan is recorded. The bins are then ranked, with rank 1 and 115 representing the lowest and highest value of the statistics, respectively. The ranks are then summed within each bin across the genome scans. The summed rank across studies is compared to its probability distribution under the hypothesis of no linkage assuming ranks are randomly assigned. This procedure provides the nominal P-value of each bin.

Follow-up studies do not, by definition, cover the whole genome. The problem is then to assign a rank between 1 and 115 to each reinvestigated bin. We applied the extension proposed by Wise.20 First, the observed maximum value of the statistics in the follow-up bin is recorded. Simulations under the hypothesis of no linkage, using the family structures, affected status, and marker information of the follow-up studies, are carried out to obtain the distribution of the maximum statistic values. The ranks the observed statistics would have are obtained from this distribution. The analysis then proceeds as above, with calculation of the summed rank across studies and of the P-value.

Of the total 115 bins, 69 (60%) were followed up: 55, 11 and three bins were available in five, six and seven studies, respectively.

Application of GSMA to Coeliac Disease data

Here, GSMA was modified for the application to the Coeliac Disease data, to account for some difficulties of the method, in particular the different linkage statistics which can be used in a genome scan, the arbitrariness of bin cutoff points and the different information content of each sample. Sensitivity of the results to those three points was evaluated.

Different linkage statistics

As originally proposed, GSMA is based on published results of studies that are not necessarily based on the same linkage statistics. Here, all four CD genome scans were carried out using different statistics. Recording the P-value of the maximum statistics for each bin in some studies was therefore difficult. Here, since the raw data were available, all samples were reanalysed with the same statistics. The statistics chosen was the Zlr of Kong and Cox23 implemented in the Allegro software.24 This model-free statistic is based on the allele-sharing among the affected individuals in the pedigree and then transformed to get an asymptotically standard normal distribution when there is no linkage. It is similar to the perhaps better known Non Parametric Linkage (NPL) statistic in Genehunter,25 but not as conservative when the meiotic information, as is the case in most real studies, is far from complete. The marker map and marker allele frequencies were those specified in the original studies. The bins were ranked according to the observed maximum Zlr value. Note that there were no tied ranks, as for each genome scan, all values of Zlr were different.

To evaluate the sensitivity of the method to the linkage statistics, we also performed the meta-analysis using the ranks obtained with the initial statistics for the Italian and Scandinavian data.

Arbitrariness of bin cutoff points

Even when there is a risk factor on the genome, the maximum statistics will often not be obtained on the exact position of the functional factor. It has been shown26 that, for a genetic risk factor with a weak effect, only one third of the maximum Maximum Lod Score (MLS)27 values are at the correct location, while as many as 14% are observed at more than 10 cM from the true position. This result also holds for the Zlr statistic. Thus, the maximum in two different studies could be observed in two contiguous bins. This is true whatever the length of the bins, if the true position is close to a cut-off point. GSMA would then fail to detect the risk factor. To minimise this problem, we propose to use an average rank (A1) over three bins, where the new rank of a bin is the average of its own rank and of the two flanking bins. Denote by R the rank of the bin under consideration and by R−1 and R+1 the ranks of the two flanking bins. Then the new rank R is computed as (R−1+R+R+1)/3. If the bin has only one flanking bin–the two most extreme bins in a chromosome, or chromosomes 21 and 22 that consist of two bins only–the average is calculated over those two bins (ie either (R+R+1)/2 or (R−1+R)/2). We investigated the sensitivity of the meta-analysis to the choice of the averaging procedure by comparing the results under another averaging (A2). In A2, the new rank of a bin R equals (R−1+2R+R+1)/4. In other words, score A1 gives equal weight to three consecutive bins, while score A2 gives more weight to the bin under consideration.

Information content

GSMA does not take into account the different information content of each study. This can be performed by weighting each rank. For the sake of simplicity, we chose to weight the individual ranks by the number of pedigrees in the data set, where extended families, as well as nuclear families with several affected sibs, contributed one unit.

We studied the sensitivity of the meta-analysis to the weighting procedure by applying another weighting score W2, where the rank of a bin in a sample is weighted by the value of the statistics observed for HLA in that sample, since HLA is known to be a genetic risk factor for CD. The comparison of the results, however, can only be made on the full genome scans since the HLA information is not available in the follow-up studies. The Zlr for HLA were equal to 5.15, 2.69, 3.99 and 5.58 in the Italian, British, Scandinavian and Finnish data sets, respectively.

Determination of P-value of each bin

For a given weighting (W1 or W2) and averaging (A1 or A2) scheme, the null distribution of the summed score across studies for a given bin is assessed as follows: for each study a simulated rank value is obtained by a random draw from the 115 observed average rank values in that study. The weighted sum across studies is then calculated. This process is repeated 50 000 times. The P-value of an observed weighted summed rank is then obtained by the number of times the observed value was exceeded by a corresponding simulated value divided by 50 000.

This procedure provides the nominal P-value for a given bin, and not the overall significance of the meta-analysis, which could only be assessed by heavy simulations. Using a Bonferroni correction, a nominal P-value of 4.3 × 10−4 would correspond to a global type I error of 5% if the bin ranks were independent. However, the observations are not independent since the ranks of adjacent bins are strongly correlated, even more so with the averaging procedure.

Mega-analysis

Mega-analysis was performed on all the pooled raw genotypes, genome scan and follow-up, using all the markers of the common map. Linkage scores were calculated as the statistic Zlr23 using the Allegro24 linkage software.

For the pooled analysis, a nominal P-value of 2 × 10−5 (as suggested by Lander and Kruglyak28) will correspond to a global P-value smaller than 5%, first because the genome scans were not performed with a dense map (average intermarker spacing about 10 cM). Moreover, the follow-up studies were performed only on a restricted number of regions chosen conditionally to the genome scans results.

Results

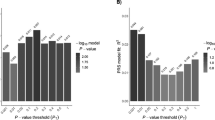
Figure 1 shows the result of GSMA with average score A1, weighting scheme W1 and the Zlr statistics, on the full genome scans and follow-up regions. Two regions are significant at a nominal 1% level.

Figure 1
figure 1

Meta-analysis of the coeliac disease genome scans and follow-up studies. Each dot represents −log(P-value) of a given bin. The vertical lines indicate the chromosome.

Full size image

The most significant region (P∼10−6) corresponds to the HLA region on chromosome 6. HLA is located in bin 42, but the effect of the HLA risk factor is so large that the two neighbouring bins (41 and 43) are also very significant. In fact, bin 42 was ranked highest in three genome scans (Italy, Finland, UK) and third highest in the Norway/Sweden one.

The second most significant region is chromosome 5qter. Overall, two bins, 39 and 40, achieve a nominal P-value of 0.003 and 0.006 respectively. Note that bin 39 and 40 were studied six and seven times, respectively. This region, found originally in the Italian study3 was also found in the Scandinavian5 and Finnish6 screens, although it did not reach statistical significance in the individual genome scans. It is of interest that the meta-analysis supports these results.

We then assessed the robustness of results to our modifications of GSMA. The three HLA bins (41, 42 and 43) and bin 39 and/or 40 on 5q were always the most significant ones, whatever the averaging and ranking procedures. Note, however, that only HLA is detected when GSMA is applied without averaging ranks. Indeed, although 5q was found in most studies, the peak statistic shifted from study to study. This is what is expected for a risk factor with moderate effect.26 Averaging ranks across adjacent bins minimises this effect and thus allows detection of 5q. Finally, the ranks obtained using the MLS for the Italian genome scan and the NPL for the Scandinavian one, did not have an impact on the results of the meta-analysis, since the rank order was the same as that of the Zlr for HLA and 5q.

The two regions found by meta-analysis are coherent with those detected by the mega-analysis. The results of the pooling method for the full genome scans and the follow-up studies are shown graphically for each chromosome in Figure 2. The best marker on each chromosome is shown in Table 1. Apart from the HLA region, only 5q31–33, with a maximum of Zlr=4.39 (P=6 × 10−6), showed genome-wide significant linkage according to standard thresholds.28 Two other regions, 11q and 14q, achieved a nominal P<0.01. The 11q region corresponds to that highlighted in the Italian3 and Scandinavian5 genome scans, while the 14q exhibited a moderate NPL in the Finnish scan.6

Figure 2
figure 2

Zlr curves of pooled analysis for each chromosome.

Full size image
Table 1 Highest linkage scores per chromosome in the pooled analysis
Full size table

Discussion

The most important result of this study is that it leaves very little doubt on the presence of a genetic risk factor involved in CD in the 5q31–33 region. Several genome scans had already pinpointed this region, without however individually achieving the recommended genome-wide level of significance. This result shows the interest of international collaboration and of joining efforts for global interpretation.

The meta-analysis by GSMA reflects the importance of taking into account the repeatability of linkage findings. One expects such a meta-analysis based on the ranks of the maximum value of a statistics to be not as powerful as an analysis, where all data are pooled and analysed as one data set. However, the two approaches gave consistent results, by giving evidence for the same two regions, HLA and 5q31–33.

The modifications we proposed in GSMA-AW attempt to address the three main difficulties of the method: the use of different linkage statistics, the bin construction and the incorporation of the information content provided by each sample.

The bins are ranked according to the scores achieved in each scan for a particular statistic. Exactly which statistic was used can be difficult to gather from the literature. Here, the situation was ideal, since the same statistic was used in all studies. However, we showed here that the most significant results were found, even with different statistics.

Similarly, HLA and 5q31–33 are detected, if the bins are attributed ranks that take into account those of adjacent bins. If no such averaging score is introduced, the significance of region 5q is considerably decreased. Indeed, in the two Italian studies, the maximum MLS values were obtained for markers in two adjacent bins, bin 40 in the genome scan (MLS=2.0 for D5S2006) and in bin 39 in the replication study (MLS=1.06 for D5S640). However, we had shown7 that under the hypothesis of a genetic risk factor with moderate effect, the probability of observing two peaks at a distance of 35 cM was not negligible and that the 95% confidence interval of the maximum MLS spanned the entire interval tested.

Weighting each rank to take into account the linkage information provided by each sample is fairly intuitive. Indeed, there is a substantial variation of the information content between different regions due to the number of families analysed, the availability of founders, marker heterozygosity, marker density and genotyping success rate. Here, each rank was weighted by the number of families, whatever their structure (nuclear or extended), and whatever their number of affecteds. We investigated the impact of another weighting scheme, based on the value of the statistic for the already known risk factor in HLA. This could only be done on the full genome scans. We showed that the results for the two most significant regions were the same with both weighting procedures.

Note that other weighting schemes could be devised. However, the optimal weights depend on the genetic model of the risk factor to detect, which is unknown.

The 5q31–qter region is interesting as it has been repeatedly highlighted in studies of several multifactorial diseases, either inflammatory, such as Crohn disease,29 abnormal immune response diseases, such as type I diabetes,30 asthma and allergy,31 as well as infectious diseases such as schistosomiasis.32 This chromosome 5 region contains many candidate genes of interest for Coeliac Disease. A candidate gene strategy is now underway by the partners of the EU cluster.