Introduction

The transmission/disequilibrium test (TDT)1 is a powerful method for testing linkage between a marker and the disease gene in the presence of association.2, 3, 4 Case–control studies compare marker-allele distributions in affected and unaffected individuals; when a significant result is obtained, it may be due to linkage or population structure. To test for linkage after obtaining a significant case–control result, within-family tests can be performed. In a TDT test, genotypes of cases are compared to those of their parents to explore whether a specific allele, or marker, at a locus of interest is transmitted to a greater degree than Mendelian inheritance would warrant. In order to integrate all available information and thereby increase the statistical power, Nagelkerke et al5 proposed a new TDT statistic by combining a TDT test and a case–control result using the generalized logistic regression.

For multiallelic markers, there are a number of extensions to the TDT after its debut.6, 7, 8, 9, 10 In this article, we develop a new approach by combining a small size TDT test and a case–control result for multiallelic markers. As a measure of association, linkage disequilibrium (LD) has a great effect on the power of the TDT test, so we explore the LD sign (positive or negative) using the case–control data, then use the biallelic TDT statistic computed for one allele subset including alleles with the same LD sign versus all other alleles combined. We find from a simulation study that it is possible to increase the power of the TDT test when the sample size is relatively small.

In the following sections, we review some existing TDT tests for multiallelic markers. Then we introduce our new approach, involving the combination of a TDT test and a case–control result. Next, we describe the steps of our proposed simulation study, and based on the simulation results we evaluate the performance of the test statistics. Finally, a few concluding remarks are given in the discussion section.

Method

We consider a random mating population in which Hardy–Weinberg equilibrium is assumed. Suppose a biallelic disease locus has alleles D and d. Consider a multiallelic marker with L alleles, M1, …, ML. Let the allele frequencies of Mi and D be pi and q, respectively; and the frequencies of haplotype MiD and Mid be hi1 and hi2, respectively. The LD between the marker allele Mi and the disease allele D is given as Δ(i)=hi1−piq. Suppose the penetrances of the disease given genotypes DD, Dd and dd are f2, f1 and f0, respectively, and Pr(A)=f2q2+2f1q(1−q)+f0(1−q)2 represents the prevalence of the disease in the population. Let θ be the recombination fraction between the marker locus and the disease locus. For i=1,…, L, j=1,…, L, let nij denote the number of those parents who transmit the Mi allele but not the Mj allele to their affected children. Let ni·=∑j≠inij denote the number of heterozygous parents who transmit the Mi allele, and let n·i=∑j≠inij denote the number of heterozygous parents who have the Mi allele but do not transmit it. Homozygous parents are not included in the sample, as they are noninformative for the transmission tests. For the allele pair Mi and Mic, the biallelic TDT statistic is given by

which asymptotically follows a χ2 distribution with one degree of freedom under the null hypothesis of no linkage.

Existing test statistics

For multiallelic markers, there are a number of extensions to the TDT test. For example, the generalized TDT (GTDT) statistic9 is proposed as,

where d′=(d1,d2,…,dL−i·), di=ni·−n·i, and V is the estimate of the variance and covariance matrix. A simpler test statistic, Tmhet,7 is given as

Under the null hypothesis, both the GTDT and Tmhet statistics follow asymptotically a χ2 distribution with L−1 degrees of freedom, and both reduce to the biallelic TDT statistic when L=2.

The maximal TDT statistic, maxTDT,9 is defined as

Since the exact and asymptotic distributions of the maxTDT are not available, the critical value at a given level of significance α is determined using the simulation method proposed by Kaplan et al.11

Combining TDT with case–control (ccTDT)

When a case–control study is carried out first and a TDT study is carried out subsequently within the same population to corroborate case–control findings independently, it is possible to combine the TDT test and a case–control comparison in order to integrate all available information, particularly when the sample size of the TDT test is not large enough to detect linkage for multiallelic markers. We try to find the LD sign of each marker allele through the prior case–control analysis so that the biallelic TDT test can be constructed through combining alleles with the same LD signs.

Suppose for simplicity m unrelated cases and m controls are sampled randomly from the population. For the multiallelic marker, let t1i and t2i, i=1, …, L, be the numbers of allele i in cases and controls, respectively. The usual χ2 test for allele i is

where t.i=t1i+t2i, is the number of allele i in both cases and controls. The frequencies of the marker allele i in the case and control groups can be calculated as follows

and similarly, Pr(Mi∣control)=pi−Δ(i) [(f2−f1)q+(f1−f0)(1−q)]/(1−Pr(A)). So the expectation of the difference of allele numbers,

is determined by the LD measure Δ(i), and it is possible to use this difference to estimate the signs of the LD. Naturally, we might expect to construct a more powerful test by grouping those alleles with positive (or negative) signs of Δ(i) as a single allele in the biallelic TDT test. The details of our TDT test combining with the case–control information, ccTDT, are given below:

Step 1: Group all L marker alleles according to the signs of their LD estimates, and suppose Λ+={j:t1j−t2j≥0}, and Λ−={j: t1j−t2j<0};

Step 2: For any allele subset G={i1,…, ig}, where 1≤g≤L, we can calculate the biallelic case–control χ2 test statistic which regards the allele sets {i1, …, ig} and {i1, …, ig}c as two single alleles,

 Step 3: Take the subset G that maximizes the biallelic χ2 test statistic for all subsets of Λ+ and Λ− as follows, that is

According to the subset G obtained by the case–control data, the usual biallelic TDT test can be constructed as

which follows a χ2 distribution with one degree of freedom under the null hypothesis of no linkage, because the subset G is determined independently by the case–control data before the TDT test is constructed.

Simulation

Simulation design

In this section, we make a power comparison between the GTDT, Tmhet, maxTDT and ccTDT tests at the α=0.05 significance level. Three disease models of inheritance are considered: (1) recessive model f2=1, f1=f0=0; (2) additive model f2=1, f1=0.5, f0=0; (3) dominant model f2=f1=1, f0=0. Suppose D is the disease allele with population frequency q=0.01, and d is the normal allele.

Since the LD is the most important factor affecting the power of the association and linkage tests for the multiallelic marker, similar to the population design of Kaplan et al11 we design the simulated populations according to the LD situation and the association index I* where

is based on the theory of testing for the equality of two independent multinomial distributions.12

In the first simulation study, we aim to investigate the performance of the test statistics under different LD situations. In all, 200 cases, 200 controls and 100 trios are taken independently from an identical population. A six-allelic marker with equal frequency p1=p2=p3=p4=p5=p6=1/6 is taken. As shown in Table 1, we consider six LD modes as (1) one positive peak; (2) two positive peaks; (3) one positive peak and one negative peak; (4) two positive peaks and one negative peak; (5) two positive peaks and two negative peaks; (6) equal LD magnitude (∣Δ(i)∣) of six LD between the disease allele and each marker allele, where the peaks are in italics. In this simulation study, we also present the frequency of replicates in which the ‘correct’ subset of positively associated markers (FC) is identified.

Table 1 LD situations for a six-allelic marker in simulated populations under recessive model
Full size table

In the second simulation study, we investigate the effect of the sample size of the case–control comparison and the TDT trios, where the equal sizes of cases and controls are taken as 50, 100, 200 or 400, and the number of trios used in the TDT tests is 50 or 100 when the recombination fraction is fixed at 0.05. As shown in Table 2, we consider the unimodal, bimodal and uniform conditional marker allele distributions in these three populations, which are analogous to the population design given by Kaplan et al.11

Table 2 Conditional marker allele distributions and LD situations for a seven-allelic marker in simulated populations under recessive model
Full size table

Simulation procedure

The steps of the simulation study are given below:

  1. 1

    Specify (a) the frequencies of L marker alleles M1, …, ML and the disease allele D, p1, …, pL and q, (b) the coefficients of LD between the marker allele Mi and the disease allele D, Δ(i), i=1, …, L in a random mating population.

  2. 2

    Sample. the genotype data of m cases and m controls, then look for the allele subset G based on the case–control result.

  3. 3

    Sample N case–parents trios by the multinomial distribution based on the transmission probabilities according to Kaplan et al11 and obtain the values of the four test statistics: GTDT, Tmhet, maxTDT and ccTDT.

  4. 4

    For each of the test statistics, reject H0 if the statistic is larger than its asymptotic or simulated critical value. The simulated critical value of the maxTDT test is obtained by 5000 replications.

  5. 5

    Repeat steps 1–4, 5000 times.

Simulation results

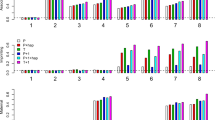
In Figure 1, we demonstrate the size and power comparison of the six LD situations for a six-allelic marker locus under the recessive model. When there is no linkage θ=0.5, all four tests control the size α=0.05 well. When there is linkage between the marker and the disease gene, for all six populations, the ccTDT test is more powerful than the other three TDT tests. We should note that for populations 1, 2 and 6, the frequencies of the replicates in which the ‘correct’ subsets of positively associated markers (FC) are identified are about 90%, while for populations 3–5 the frequencies are much lower. Nevertheless, in almost 100% of the replicates the positive and negative LD peaks are classified correctly for the latter populations (results omitted). All tests achieve the highest power under the recessive model, but each performs similar for both the additive and the dominant models (results not shown). For the TDT tests on multiallelic markers, the GTDT and Tmhet are found to have a similar performance and achieve a higher power when several alleles are more or less equally associated.

Figure 1
figure 1

Power comparisons of the GTDT, Tmhet, maxTDT and ccTDT tests for populations 1–6 given in Table 1 under the recessive model. FC is the frequency of replicates in which the ‘correct’ subset of positively associated markers is identified. The number of the cases, controls and trios are 200, 200 and 100, respectively. The power is based on 5000 replications.

Full size image

In Figure 2, we investigate the effect of the size of the case–control sample, that is, 50, 100, 200 and 400, to the small trio size (a) 50 and (b) 100. Since the case–control samples are not used by the GTDT, Tmhet and maxTDT tests, their power curves in Figure 2 are almost horizontal (they are not entirely horizontal due to simulation variation). For populations 8 and 9, the ccTDT test has a better performance than the other tests when the numbers of cases and controls are larger than 50 and 100 and the number of trios are 50 and 100, respectively. However, for population 7, the ccTDT test does not outperform the others until the numbers of cases and controls increase to 200. As the sample size of the case–control increases, the power of the ccTDT test increases as well (Figure 2).

Figure 2
figure 2

Power comparisons of the GTDT, Tmhet, maxTDT and ccTDT tests for populations 7–9 given in Table 2 under the recessive model for θ=0.05. The equal sizes of the case–control are 50, 100, 200 and 400, which are, respectively, denoted as 1, 2, 3 and 4 in the x-axis. The numbers of trios are (a) 50 and (b) 100. The power is based on 5000 replications.

Full size image

Discussion

In this article we investigate an extension of the TDT test, utilizing the available information of a case–control study in order to increase the statistical power of a TDT test with a small-sized sample. As shown by several investigators, the TDT test is valid for linkage detection when LD exists, and the power of the TDT test depends on the magnitude of LD.6, 8, 11 Based on this property, we develop a new test under Hardy–Weinberg equilibrium, ccTDT, which uses the biallelic TDT statistic computed for one allele subset including alleles with the same sign of LD versus all others combined based on the information of a case–control sample. A nice property of ccTDT is that its asymptotic distribution is known and the critical value can be easily determined, which is not the case for maxTDT.

The simulation findings demonstrate that the ccTDT performs well for the small-sized trios, but also performs more powerfully as the size of the case–control sample increases. The test is expected to have a good power, especially for bimodal and uniform models.