Introduction

During transmission X-ray scattering measurements, the sample is often placed into a capillary tube and set in a sample holder that has holes for the X-ray path, as schematically shown in Figure 1a. This cell will hereafter be called ‘cell-A’. If precise control of temperature is required, the sample holder is heated or cooled. In this type of cell, there is always a thermal gradient around the ‘probe windows’, which are the holes designed for X-ray illumination of the sample and for the measurement of the scattered X-rays. In many cases, this thermal gradient is considered to be negligible and is consequently not seriously considered. If the sample is held under a gas, such as air, the thermal gradient may not be essential because there are heat transfers or convections of the gas. However, if the cell is used under vacuum, the thermal gradient in the holder may have a considerable role in the thermodynamical properties of the system, such as dynamical properties of the sample.1, 2 Specifically, during dynamical studies of polymers, the temperature of the sample is sometimes elevated above the glass transition temperature, and the sample is maintained under vacuum to prevent oxidation. In such cases, the thermal gradient problem is significant.

Figure 1
figure 1

Schematic illustration of the sample cells for the X-ray photon correlation spectroscopy (XPCS) studies of polystyrene (PS)-grafted silica nanoparticles (SiNP-PSs) in a PS matrix. In cell-A, the sample is kept in a capillary tube (a). In cell-B, the sample is sandwiched by aluminum foil with a Teflon spacer (b). Both cells are heated in a vacuum of ∼100 Pa.

Full size image

To reduce this thermal gradient effect, the size of the probe window could be minimized. However, the window needs to be sufficiently large to acquire X-rays scattered at large angles. Therefore, there is always a compromise between these two opposing factors during the design of a cell.

X-ray photon correlation spectroscopy (XPCS), which measures the dynamics of scatterers from the fluctuation of coherent scattering, is one of the most sensitive methods for detecting this dynamical aspect of polymers. In the present work, we studied the possible effects for the formation of a thermal gradient using XPCS with a model system of polystyrene (PS)-grafted silica nanoparticles (SiNPs-PS) in a PS matrix.

This paper is organized as follows. The experimental methods are explained in Experimental procedure. In Static properties of the SiNPs-PS in a PS matrix Section, the static conditions of the samples studied by small-angle X-ray scattering are shown. The dynamical behavior of the SiNPs-PS in cell-A studied by XPCS is shown in Dynamical behavior in cell-A Section, and the XPCS data for the newly designed cell with a minimum thermal gradient are shown in Dynamical behavior in cell-B Section. The conclusions are presented in Conclusions.

Experimental Procedure

Sample preparation

The SiNPs-PS were prepared using the ‘grafting-from’ method. First, the surface-initiator BHE ((2-bromo-2-methyl) propionyloxyhexyltriethoxysilane)3, 4 was immobilized on a SiNP (110 nm diameter; Nissan Chemicals, Tokyo, Japan) in ethanol in the presence of a 5% ammonia solution at 313 K for 12 h. The BHE-coated SiNPs were purified by consecutive centrifugation and redispersion in dimethylacetamide to obtain a stock dimethylacetamide suspension. Subsequently, surface-initiated atom transfer radical polymerization of styrene was conducted from the BHE-coated SiNPs in dimethylacetamide using CuBr and N,N,N′,N′′,N′′-pentamethyldiethylenetriamine at 333 K for 48 h. The number averaged molecular weight, polydispersity and graft density of the grafted PS were Mn=2.30 × 104 g mol−1, Mw/Mn=1.41 and 0.28 chains per nm2, respectively; these parameters were determined using size exclusion chromatography of the PS obtained from the hydrolysis of the SiNPs-PS. The resultant suspension was centrifuged and then redispersed in tetrahydrofuran to isolate the SiNPs-PS. The resultant particles and bulk PS (Mn=1.05 × 104, Mw/Mn=1.09) were dissolved in tetrahydrofuran and air dried to prepare the SiNPs-PS dispersed in a PS matrix. The silica concentrations in the PS matrix were adjusted to be 0.24, 0.96 and 5.04 vol%; these samples are hereafter called sample-A, sample-B and sample-C, respectively. The SiNPs-PS of these samples were determined to be aggregated, as mentioned below. We also prepared a non-aggregated sample with a concentration of 0.96 vol%, named sample-D, whose SiNPs-PS and PS matrix are same as those of sample-A, -B and -C.

The static behavior of the sample was investigated using ultra-small-angle X-ray scattering (USAXS). The USAXS experiments were performed at the BL19B2 beamline of SPring-8 with an incident X-ray wavelength (λ) of 0.0689 nm and a sample-to-detector distance of 41 890 mm. The static properties in the larger spatial scale, which could not be covered by USAXS, were examined using laser scanning confocal microscopy with a Zeiss LSM510 (Oberkochen, Germany). Through these optical measurements, we confirmed that there were no aggregates with a diameter larger than 1 μm (see Supplementary Information). The viscosity of the PS matrix was measured using a rotational rheometer (MCR302, Anton Paar, Graz, Austria).

X-ray photon correlation spectroscopy

The XPCS measurements were performed on the BL19LXU beamline with a 27-m-long undulator at SPring-8 (Hyogo, Japan).5 The undulator source and the Si(111) monochromator were tuned to an energy of 8.00 keV, and the higher harmonic X-rays were removed using Pt-coated mirrors. The transverse coherence of the incident X-rays, ξt∼16 × 132 (H × V) μm2 at the sample position, was ensured by the use of slits with a width of 20 μm × 20 μm. The parasitic scattering was shielded by the use of additional slits and a pinhole, and the partially coherent X-rays were illuminated to the sample in vacuum. The scattered X-rays were detected using a PILATUS 100 K (DECTRIS, Baden, Switzerland) two-dimensional hybrid pixel array detector with the grid mask resolution enhancer mounted ∼3.5 m downstream of the sample.6 For every measurement, 5000–20 000 images were collected with an exposure time of 30–100 ms followed by a readout time of 3 ms. To examine the experimental conditions between different beam times, such as contrast, the same sample, which consisted of silica particles suspended in polypropylene glycol with an average molecular weight of 4000 g mol−1 (PPG4000; Wako Chemical Co., Ltd, Osaka, Japan) at a volume fraction of 0.5 vol% sealed in a Lindemann glass capillary tube, hereafter called Si/PPG, were measured at every beam time.

During the XPCS experiments, after maintaining the sample at the measured temperature, the XPCS measurements were repeated every 30 min until no further change was observed. After completing the measurement at all of the temperatures, the measurement was performed at the first measured temperature again to confirm that there was no damage from the X-ray illumination.

Sample Cells

Two types of sample cells, that is, cell-A and cell-B, were prepared for the present study. Figure 1a shows a schematic illustration of cell-A. When using cell-A, the sample was held in a 10-μm-thick quartz capillary tube with a diameter of 2 mm, which was placed in a copper block with probe windows (incident side: 1 mm in diameter, scattered side: 3 mm in diameter). The temperature of the sample was controlled by heating the entire cell under vacuum (∼100 Pa). The XPCS measurements of sample-A, -B and -C were performed using cell-A.

Figure 1b shows a schematic illustration of cell-B, in which a Teflon spacer (1.5 mm-thick) was sandwiched by two aluminum foils (12 μm-thick), and the entire cell was covered by copper blocks. The sample was held in a space created by the Teflon spacer, and the temperature was controlled in the same manner as cell-A.

Results and discussion

In this section, the results from the experimental studies of the SiNPs-PS in a PS matrix (sample-A, -B, -C and -D) are presented and discussed. The static properties of the samples, which were studied using USAXS, are presented in Static properties of the SiNPs-PS in a PS matrix Section. The dynamical behavior of sample-A, -B and -C in cell-A studied using XPCS is shown in Dynamical behavior in cell-A Section, and the dynamical behavior of sample-D in cell-B studied using XPCS is presented in Dynamical behavior in cell-B Section.

Static properties of the SiNPs-PS in a PS matrix

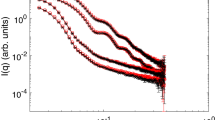
Figure 2a presents the USAXS intensity profiles, I(q), of sample-A, -B and -C, which show characteristic fringes from the primary particle, the form factor from the particles, at the high q region (q>5 × 10−2 nm−1). In theory, the form factor should be flat as q→0. However, the I(q) plots of sample-A, -B and -C were not flat, but rather I(q) increased as q→0. This experimental result suggests that the SiNPs-PS of sample-A, -B and -C aggregate in the PS matrix. As the only difference between sample-A, -B and -C is the concentration of the SiNPs-PS, the size of the aggregates in these samples may be the same, at least as a first approximation. Therefore, the sizes of the aggregates of sample-A, -B and -C were estimated from the Guinier analysis of the I(q) of sample-A, which was the most dilute system of the three systems, and the sizes of the aggregates were determined to be >245 nm in radius. Whereas the I(q) of sample-B is almost the same as that of sample-A, the I(q) of sample-C is clearly different from that of the other two samples, especially in the low q region. This suppression of scattering intensity may be due to the interparticle scattering effect in the highly concentrated sample-C.

Figure 2
figure 2

Scattering intensity profiles of polystyrene (PS)-grafted silica nanoparticles (SiNP-PSs) in a PS matrix obtained through ultra-small-angle X-ray scattering (USAXS) measurements. The profiles of sample-A, -B and -C are plotted in (a), and that of sample-A is plotted in (b). The solid line depicted in (b) is a fitting curve by a form factor of a spherical particle.

Full size image

The small-angle X-ray scattering intensity profile of sample-D is shown in Figure 2b. This profile can be expressed by the form factor of a sphere given by a Gaussian size distribution with a mean radius of 54.9 nm and a root mean square deviation of 4.1 nm, as depicted by the solid line in Figure 2b, demonstrating that the silica particles are well-dispersed in the PS matrix without the formation of aggregates.

Dynamical behavior in cell-A

During XPCS measurements, the fluctuation of the scattering intensity, I(q,t), at a scattering vector, q, is obtained in a time series t, and the intensity time-autocorrelation function g2(q, t) is evaluated as

where the angle brackets indicate time-averaging. In the present study, the scattering data were analyzed separately depending on the direction with respect to the long axis of the capillary tube, as shown in Figure 3, where the direction with respect to the long axis of the capillary tube is defined as ‘parallel’, and the vertical direction to that axis is defined as ‘perpendicular’. Taking the elongated shape of the samples into consideration, the thermal gradient may be more remarkable in the parallel direction than in the perpendicular direction, if any. To examine the thermal gradient effect on the motion of the scatterers, the obtained data from the parallel pixels, , and the data from the perpendicular pixels, , were averaged separately over all pixels within the complete range of q=0.45 × 10−2 nm−1.

Figure 3
figure 3

Schematic view of the separate analyses dependent on the direction. The parallel direction is parallel to the long side of the capillary tube, and the perpendicular direction is perpendicular to that side. The pixels along the parallel direction from the beam center and the pixels along the perpendicular direction from the beam center are analyzed separately.

Full size image

Figure 4 shows various and of sample-A, -B and -C at 463 K as representative examples of the dynamical behavior of the SiNPs-PS in cell-A. As shown in Figure 4a, the of sample-A at 463 K decayed faster than the at all measured q values. These results clearly demonstrate that the dynamical behavior of the SiNPs-PS of sample-A is anisotropic, and the motion of the SiNP-PS in the parallel direction is faster than that in the perpendicular one. As shown in Figure 4b, of sample-B at 463 K, whose concentration of SiNP-PS is four times greater than that of sample-A, also damped faster than at all measured q values. However, the difference between and of sample-B is smaller than that of sample-A. These behaviors of and of sample-A and sample-B are observed at all measured temperatures. In contrast, no difference was observed between and for sample-C at 463 K (Figure 4c). Although this isotropic dynamical behavior was observed in sample-C at all measured q values at 463 K, at temperatures >463 K, damped slightly faster than . From these results, one can conclude that the SiNPs-PS motions of sample-A, -B and -C in cell-A are basically anisotropic, and the degree of anisotropic behavior has a dependence on the concentration of the SiNP-PS. For more quantitative discussions, the measured data are analyzed using the fitting method described below.

Figure 4
figure 4

Representative results of (closed circle) and (open circle) for sample-A (a), sample-B (b) and sample-C (c) obtained at 463 K. Dotted lines are fitting curves using Equation 2, and solid lines are fitting curves using Equation 4. The dashed-dotted line in (a) q//=1.68 × 10−2 nm−1 is the fitting curve using Equation 2.

Full size image

First, the perpendicular data are fitted with the exponential form

where A and Γ are the speckle contrast and the relaxation rate, respectively. As shown by the dashed lines in Figure 4, Equation 2 expresses all of the measured well. The hydrodynamic radius was estimated by Stokes–Einstein equation from measured at each temperature. However, the estimated values seemed to be too large and varied between 500 and 800 nm, which might be caused by the difference of viscosity due to the thermal gradient. Thus, we checked the size of the aggregates by laser scanning confocal microscopy. In these experiments, A∼0.01 was obtained. The same value of A was also obtained from the standard sample of Si/PPG during the beam time. Therefore, the value of 0.01 was specific for that experimental condition, and the reduction of A caused by the dynamics that were faster than the frame rate, such as the motion of the primary particles, is negligible.

The parallel data also exhibited damping behavior. However, the measured were not well fit using Equation 2, as shown in the representative fitting curve in Figure 4a at q=2.98 × 10−2 nm−1 with the dashed-dotted line. Therefore, the parallel motion of the SiNP-PS should be somewhat different from the perpendicular motion. Considering the general trend of the above experimental results in , which decays faster than , the parallel motion has other components in addition to the components of perpendicular motion. In one of the simplest cases, the parallel motion component has a uniform velocity distribution in the capillary tube, as illustrated in Figure 5a. However, in this case, there should not be a change in the measured autocorrelation functions during a homodyne measurement, such as the present measurement.7 Therefore, the velocity distribution should have a gradient with respect to the direction perpendicular to the incident beam. Here, let us assume the parabolic velocity distribution as follows:

Figure 5
figure 5

Schematic illustrations of the velocity distributions of the parallel motion of polystyrene (PS)-grafted silica nanoparticles (SiNP-PS). The uniform velocity distribution (a) and the parabolic velocity distribution Equation 3 (b) in the capillary tube are drawn, respectively.

Full size image

where r is the distance from the center of the capillary, R is the radius of the capillary and v0 is the velocity at the center (Figure 5b). In this case, can be obtained using the error function8

In the analysis using Equation 4 to fit the measured data, we adopted a global fitting procedure. Namely, at each temperature, ∼10 spectra at various q values were simultaneously fitted with Equation 4 while the same fitting parameter of v0 was shared between these data sets. Γ was fixed to the values obtained from the analysis of the perpendicular data because the parallel motion is assumed to be composed of two components: one is the isotropic motions, which are the same as those of the perpendicular motion; and the other is the drift motion, which is unique to the parallel motion. The front factor, A, was varied for each q value. At all measured q, temperatures and concentrations, the measured were well fit, as demonstrated by the solid lines in Figure 4a and b. Therefore, the parabolic velocity distribution of Equation 3 (or in Figure 5b) may express the parallel motion of the SiNP-PS in cell-A.

The values of v0 obtained through the fitting analysis with Equation 4, such as 22.3 nm s−1 for sample-A and 12.9 nm s−1 for sample-B at 463 K, are plotted against temperature in Figure 6. These values exhibited remarkable temperature and concentration dependences: v0 increases with temperature and decreases with concentration.

Figure 6
figure 6

Temperature dependence of v0 for sample-A, -B and -C obtained by fitting analysis with Equation 4.

Full size image

One of the possible origins of the anisotropic motion that can easily be imagined is the sedimentation of the SiNPs-PS. The sedimentation speed, vsed, in a dilute system can be calculated using the Stokes relationship

where Rh is the hydrodynamic radius, ρ is the particle density, ρ0 is the matrix density, g is the acceleration of gravity and η is the viscosity of matrix. Here, the size of the aggregates were confirmed to be <1 μm in diameter using laser scanning confocal microscopy, and η was obtained from the measurements using a rheometer. ρ can be roughly estimated to be same as for silica particles, ∼2.2 g cm−3, and ρ0 is the density of PS, ∼1.0 g cm−3. For example, by substituting Rh=500 nm, ρ=2.2 g cm−3, ρ0=1.0 g cm−3 and η=8.06 Pa s (at 463 K) into Equation 5 as representative values, we obtain vsed=0.08 nm s−1. In reality, vsed should be smaller than this value because Rh <500 nm in our experimental system. The estimated value of vsed is considerably smaller than that of v0=22.3 nm s−1 for sample-A, which is the most dilute sample, at 463 K. At all of the other measured temperature, vsed is estimated to be <1% of the v0 of sample-A. Therefore, the possibility of sedimentation being the origin of the anisotropic motion is excluded.

Another possible origin of the anisotropic motion is the thermal convection driven by the thermal gradient inside of the cell. The critical Rayleigh number for thermal convection to occur when both the top and bottom surfaces of a fluid are free is known as

where α is the coefficient of thermal expansion of the fluid, d is the characteristic length, κ is the thermal diffusivity of the fluids, and ΔT is the temperature difference.9 By substituting the typical values of our sample, α=6.0 × 10−4 K−1, κ=5.0 × 10−8 m2 s−110 and d=2 mm (the average size of the probe windows), into Equation 6, ΔT >5.6 × 103 K is obtained. However, this value is too large, even with cell-A. Therefore, the possibility of thermal convection being the origin of the anisotropic motion is also excluded.

Another type of anisotropic behavior driven by a thermal gradient is the Soret effect. In a dilute system, the thermodiffusive drift velocity, vT, depends linearly on the temperature gradient, T, with a proportionality constant that equals the thermodiffusion coefficient DT: vT=−DT∇T.1 In this case, even a slight thermal gradient can cause thermal transport, which can be a potential origin of the observed anisotropic motion. Furthermore, a reduction of vT was reported at high concentrations in those phenomena,11 which also agree with our experimental observations.

As the thermal gradient is the consequence of the temperature decrease around the probe windows, we performed experiments using cell-B, which is expected to eliminate the thermal gradient.

Dynamical behavior in cell-B

The dynamical behavior of the SiNPs-PS of sample-D held in cell-B was examined using XPCS. As described above, the primary difference between cell-A and cell-B is the probe windows for the X-ray path. Although the detected intensity decreases by 14% compared with the quartz capillary tube in cell-A due to the X-ray absorption by the aluminum windows of cell-B, the thermal gradient around the windows is expected to be negligibly small.

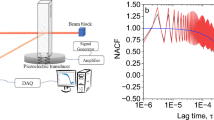
Figure 7 shows the measured and for sample-D in cell-B at various temperatures, which demonstrates the isotropic behavior of the SiNP-PS in the cell. In these experiments, A∼0.02 was obtained. The same value of A was also obtained from the standard sample of the Si/PPG during that beam time. Therefore, the difference in the A values when using the quartz cell (previous section) and using the aluminum foil was caused by the different experimental conditions. Note that the effect of using windows of aluminum foil, such as diminished contrast, did not appear to be different from that of the quartz cell.

Figure 7
figure 7

Representative results for (closed circle) and (open circle) for sample-D in cell-B at various temperatures.

Full size image

When discussing the difference between the data obtained from sample-D in cell-B and the data from sample-A, -B and -C in cell-A, the effect of particle size should be taken into consideration. According to a couple of studies, the thermodiffusive drift velocity has been shown to be proportional to the particle size.12, 13, 14 In the present case, the radius of the SiNP-PS of sample-D, ∼55 nm, corresponds to ca. 10–20% of that of sample-A, -B and -C, ∼245–500 nm. Therefore, the v0 in the parallel direction of sample-D can be estimated to be ca. 20–40 nm s−1 at 493 K if the thermal gradient effect is the same as sample-B, whose concentration is the same as sample-D in cell-A, which is large enough to be detected. However, no anisotropic behavior was observed in the motion of the SiNPs-PS of sample-D in cell-B at all measured q values and temperatures. Therefore, one can conclude that the anisotropic behavior observed in cell-A was caused by a thermal gradient around the probe windows.

Conclusions

We report experimental results from dynamical studies of SiNPs-PS in a PS matrix using XPCS with two different types of cells for temperature control under vacuum. Anisotropic motion of the SiNP-PS was observed when the sample was kept in a cell using a capillary tube (cell-A), and we demonstrated that the thermal gradient around the probe windows caused the anisotropic dynamical behavior. We also estimated the drift velocity using a parabolic velocity distribution. To confirm that the anisotropic behavior was caused by the thermal gradient, the experiment was performed using another cell (cell-B) that was designed to minimize this thermal gradient. In the experiment using cell-B, no anisotropic behavior was observed. Therefore, we can conclude that the anisotropic behavior observed in cell-A was caused by the thermal gradient around the probe windows.