Introduction

Polymer composites are widely used in daily life; for example, tire rubber, sealant and damping material are indispensable to vehicles. In general, these consist of polymers and nanoparticles. The addition of nanoparticles improves the mechanical properties, which is called the reinforcement effect. An understanding of the mechanism of the reinforcement effect is required to develop high-performance polymer composites. The properties of the composites depend on the spatially inhomogeneous deformation of the polymer, which is related to the three-dimensional (3D) structural configuration of the nanoparticles. The configuration of nanoparticles in a composite is affected by the particle diameter, aggregate structure, surface energy and interaction between the particles and the polymer. To elucidate the nature of the reinforcement effect, it is necessary to investigate the local deformation of the polymer matrix and the hierarchical 3D structural configuration of nanoparticles over a wide-size scale.

We have utilized ultra-small-angle X-ray scattering to observe changes in the aggregate/agglomerate structure of nanoparticles in uniaxially stretched rubber.1, 2 The ultra-small-angle X-ray scattering results showed that the inhomogeneous structural changes of aggregates/agglomerates have a key role in determining the characteristic mechanical/viscoelastic properties of polymer composites. Further simulation studies based on structural knowledge will help elucidate the mechanism; however, real-space 3D structural information cannot be directly obtained with a scattering technique. Thus, the development of a real-space microscopy technique is required.

Recently, a number of microscopy techniques, such as atomic force microscopy and transmission electron microscopy, have been utilized to observe fine structures in materials. The technological evolution of transmission electron microscopy tomography (TEMT) is quite remarkable; this technique has been successfully applied to observe the 3D structure of nanocomposites.3, 4, 5 X-ray imaging techniques have also been developed in association with advances in synchrotron X-ray technology. The advantages of X-ray imaging include a wider field of view, sub-micron-level spatial resolution and less damage to the specimen compared with electron microscopy.6, 7 Nusser et al.8 reported a micron-scale silica dispersion state in styrene-butadiene rubber composite observed by X-ray microscopy with synchrotron radiation, but the spatial resolution is not high enough to observe the detailed configuration of the particles. Thus, further improvements in the spatial resolution are required to visualize the 3D structural configuration of nanoparticles.

In this study, the 3D structural distribution of spherical silica particles in rubber was visualized with a higher spatial resolution using a Zernike-type phase contrast X-ray microscope than is possible with the projection CT without imaging optics such as Fresnel zone plate (FZP). Based on the results, the inhomogeneous deformation of the rubber matrix was visualized with the finite element method (FEM).

Experimental Procedure

Materials

Silica-filled styrene-butadiene rubber was used in this study. The sample recipe is shown in Table 1. The styrene-butadiene rubber contains a styrene/butadiene ratio of 23.5/76.5, which was purchased from Nippon Zeon Co. (Tokyo, Japan). The diameter of the spherical silica particles was 500 nm, and they were purchased from Nippon Shokubai (Osaka, Japan). Their size distribution is <10%. To disperse silica particles in rubber, a silane-coupling agent (Si69) purchased from Degussa GmbH (Hanau, Germany) was used.

Table 1 Sample recipe (weight ratios normalized with SBR)
Full size table

The ingredients were mixed by an internal mixer until the temperature of the compounds reached 150 °C. The compound was vulcanized at 170 °C for 12 min by a heat-pressing machine. To perform X-ray CT measurements, the rubber composites were cut into 50 (W) × 100 (D) × 1000 (H) μm3 by using a cryomicrotome.

Imaging methods

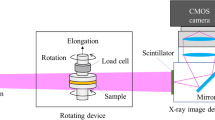
Quasi Köhler-illumination transmission X-ray microscopy (KTXM) and Zernike-type phase contrast X-ray microscopy (ZPXM) were carried out at BL47XU, SPring-8 (Hyogo, Japan).7 A schematic view of the experimental setup is shown in Figure 1. An 8-keV X-ray monochromated by a Si 111 double crystal was used. As the highly coherent X-ray degrades the image quality owing to speckle-like noise, a beam diffuser was installed in front of the sample to reduce the spatial coherence. The beam diffuser, made of carbon powder, was continuously rotated during the measurement. The microscope system was composed of a FZP and a circular condenser plate (CCP) made of tantalum. The CCP, which consists of diffractive gratings with a 200-nm line width, was installed between the beam diffuser and the sample, and it worked as a condenser for the quasi Köhler-illumination. The diameter and the thickness of CCP were 500 and 1 μm, respectively. The FZP with an outermost zone width of 100 nm was used as the objective. The diameter and the thickness of the FZP were 155 and 1 μm, respectively. The zone material was tantalum that is 1 μm thick. The Zernike phase plate (ZPP) is made of tantalum 0.96 μm thick, and the line width of the ring pattern is 4 μm. The ZPP was placed at the back focal plane of the FZP. The ZPP worked as a λ/4 phase shifter for 8 keV X-rays. This illumination system made it easy to introduce the ZPXM mode by simply installing the ZPP. The principle of the Zernike phase contrast method is that the filtering of the Fourier spectrum of the object forms at the back focal plane.9 A quasi Köhler-illumination system like this is suitable for the Zernike phase contrast method because the diffracted X-ray of the object and the nondiffractive X-ray (0th-order) are spatially sorted at the back focal plane. To block the nondiffractive X-ray (0th-order) from the CCP and the FZP, the diaphragm and the ring-shaped beam stop made of lead are placed at the front of the sample and the imaging detector, respectively. A cooled camera C4880-41S (Hamamatsu Photonics Ltd, Shizuoka, Japan), coupled with relay lenses and a scintillator (P43) screen, was placed at the image plane. The CCD camera was used under the 2 × 2 binning mode, and the camera format was 1288 × 676 pixels. To obtain the 3D structure of silica particles in the rubber composite, the sample was rotated 180° in increments of 0.1°. The reconstruction with the 1800 projection images was performed by a filtered back projection method.

Figure 1
figure 1

A schematic view of the Quasi Köhler-illumination transmission X-ray microscopy (KTXM) and the ZPXM experimental setup.

Full size image

FEM simulation method

To visualize the local deformation of rubber in the composite, an FEM analysis was performed. The eight-chain model proposed by Arruda and Boyce10 was used as the constitutive equation of FEM. The viscoelastic property of rubber caused by relaxation of the polymer chain was represented by the combination of the eight-chain model and the viscous component, as proposed by Bergström-Boyce.11, 12 The 3D FEM model consisted of hexahedral meshes and was constructed based on the results of the X-ray imaging. In addition, a homogenous FEM model in which the silica particles were stacked on the grid was performed to investigate the effect of silica conformation. The FEM simulation size was ∼6000 nm on a side, and the FEM simulations were calculated up to a strain of 75%.

Results and discussion

Visualization of the 3D configuration of silica particles

Figure 2 (left) shows the projection image of the sample. As is reported in Takeuchi et al.7, the optics of KTXM uniformly illuminates the objective. The large fluctuation in the grayscale results from the overlap of silica particles along the depth direction. The spatial resolution Δr of the imaging optics system is related to the scattering angle θ via the following relationship:

Figure 2
figure 2

(Left) The projection image observed by the Quasi Köhler-illumination transmission X-ray microscopy (KTXM) and (right) the projection image observed by the ZPXM.

Full size image

where λ, N.A., n and c are the wavelength, numerical aperture, refraction index and apparatus constant, respectively. By using a quasi Köhler-illumination system, a higher angle scattering contributes to the image formation; this leads to the improvement of the spatial resolution. In this study, the spatial resolution is estimated to be ∼120 nm.6, 7 Despite the high spatial resolution, the silica particles are barely recognizable in the projection image. The slice image of the KTXM system reconstructed by the computed tomography technique is shown in Figure 3 (left). Although the edge of silica particles is enhanced due to the refraction at the interface between silica particles and the rubber matrix, the contrast between the silica particles and the rubber matrix in the slice image is not high enough to accomplish a 3D structural determination of the silica particles’ distribution in rubber. This lack of contrast in the images originates from the low X-ray absorption of silica particles because of the size of the silica particles.

Figure 3
figure 3

Slice images of the (left) Quasi Köhler-illumination transmission X-ray microscopy (KTXM) and (right) ZPXM systems reconstructed by the computed tomography technique. An enlarged view of KTXM is shown in the inset of the left figure.

Full size image

The contrast of the images was enhanced using the ZPXM system, as shown in Figure 2 (right). In this projection image, the silica particles are clearly recognizable. The reconstructed slice image also shows a much-improved contrast, as shown in Figure 3 (right). The intensity profile and its differential profile at a typical line of the slice image are shown in Figure 4. The contrast between silica particles and the rubber matrix in the ZPXM system is approximately three times as large as that of KTXM. The FWHM of the differential profile was 297.6 nm. This indicates that the spatial resolution in the reconstruction is lower than that in the projection. This decrease of the spatial resolution could be caused by the slight oscillation of the rotation stage during the measurement. In the slice image of ZPXM, dark ‘particles’ are recognized. This indicates the existence of voids, although further study is required to confirm the existence of voids. The magnified slice images obtained by KTXM and ZPXM measurements are shown in Figure 5. The silica particles that are not recognized in the slice image with KTXM are clearly observed by the ZPXM measurement, as shown by the white arrows in the figure. The volume-rendering images after the binary image processing of slice images obtained by KTXM and ZPXM measurements are shown in Figure 6. The volume-rendering size is ∼12 μm on a side. The separation between the silica particles and rubber matrix in the KTXM volume rendering was not possible. By contrast, the silica particles are clearly observed in the ZPXM volume rendering owing to the high contrast between silica particles and the rubber matrix. From this result, we conclude that (i) the contrast between silica and rubber available with the KTXM measurement is not high enough to visualize the 3D configuration of silica particles in rubber and (ii) the use of ZPXM is a key to visualize the 3D configuration of silica particles in the rubber matrix, which is crucial to the FEM simulation.

Figure 4
figure 4

(Left) The opened circles and the closed triangles are the intensity profiles of ZPXM and Quasi Köhler-illumination transmission X-ray microscopy (KTXM) slice images. (Right) The opened circles and the solid line are the derivation profiles and the result fitted by the Gaussian function at the typical line of slice images. A full color version of this figure is available at Polymer Journal online.

Full size image
Figure 5
figure 5

The magnified slice images obtained by (left) Quasi Köhler-illumination transmission X-ray microscopy (KTXM) and (right) Zernike-type phase contrast X-ray microscopy (ZPXM) measurements.

Full size image
Figure 6
figure 6

The volume-rendering images after the binary image processing of slice images obtained by (left) Quasi Köhler-illumination transmission X-ray microscopy (KTXM) and (right) ZPXM measurements.

Full size image

To improve the quality of reconstructed images obtained by the ZPXM measurements, one should reduce the oscillation of the rotation stage during the measurement. The influence of the oscillation can be generally reduced using image correction with the fiducial marker method that is used for TEMT measurements.13 This method is, however, difficult in the present case because it is difficult to distinguish the marker particles from the silica particles that overlap them.

Visualization of local deformation of the rubber matrix

To understand the local deformation of matrix rubber in the composite at the microscopic scale, we carried out an FEM simulation analysis. The 3D structural configuration of silica particles determined by the ZPXM measurement was used for the FEM simulation model. The surface of the silica particles was processed smoothly. In addition to the actual inhomogeneous FEM model based on the ZPXM result, the homogenous FEM model in which silica particles were stacked on the grid was prepared to investigate the effect of the silica configuration on the local deformation of the rubber matrix. Figure 7 shows the 3D FEM calculation results at a strain of 75%. Typical cross-sectional surfaces of the FEM simulation results are shown in Figure 8. The rubber between neighboring silica particles in the actual model showed larger deformations than the homogenous silica model. The local deformation ratio at the microscopic scale became several times larger than the bulk deformation ratio, and a network of strain was formed through the silica particle. From the above results, it is speculated that the increase in the mechanical properties, such as the strength of the composite, originates from the localized large deformation of rubber on the microscopic scale. In this way, the visualization of local deformation with the FEM analysis provides important information about the influence of the silica distribution on the improvement of the mechanical properties of the rubber composite. Further investigations with the FEM simulation combined with X-ray imaging will offer significant insight into the relationship between the microscopic structure and macroscopic viscoelastic properties. K. Akutagawa et al.14 reported a similar study using the combination of TEMT and FEM.14 TEMT has a higher spatial resolution than ZPXM, and the FEM simulation based on TEMT is therefore a powerful tool to clarify the effect of particle size, form and aggregation structure of particulate silica in rubber, whereas ZPXM is suitable for the observation of the high-order structure of particulate silica, such as agglomerates, because the field of view of ZPXM is wider than that of TEMT. In future, a combination of ZPXM and TEMT will become increasingly important for developing an understanding of the detailed structure of nanocomposites.

Figure 7
figure 7

The three-dimensional (3D) finite element method (FEM) calculation results at a strain of 75%; (left) inhomogeneous FEM model and (right) homogeneous FEM model. A full color version of this figure is available at Polymer Journal online.

Full size image
Figure 8
figure 8

Typical cross-sectional surfaces of the finite element method (FEM) calculation results at a strain of 75%; (upper) inhomogeneous FEM model and (lower) homogeneous FEM model. A full color version of this figure is available at Polymer Journal online.

Full size image

Conclusion

We visualized the strain field of a polymer matrix using an FEM simulation based on knowledge of the 3D structural configuration of silica particles in rubber. The 3D structural configuration was obtained by using the Zernike-type phase contrast X-ray imaging method. The Zernike-type phase contrast X-ray imaging method improved the contrast of images and gave us an opportunity to investigate a detailed 3D-submicron scale configuration of particles with a wide field of view. This method is proven to be a powerful tool to obtain the 3D structural configuration of nanoparticles in a composite. Based on the structural information, the inhomogeneous local deformation of the rubber matrix was visualized using FEM simulations. Further improvement will enable us to observe smaller nanoparticles, which will provide valuable information about the differences in percolated network structures affected by the surface energy of nanoparticles and interactions between nanoparticles and polymers.