Introduction

The viscosity of supercooled liquids increases dramatically upon cooling, leading to vitrification. Such massive and continuous increase in viscosity is essential to the glass transition behavior, but its mechanism is not fully understood.1, 2, 3, 4 One important feature is that the viscosity (or the relaxation time of segmental motions) depends on configurational entropy. This view is closely related to the picture of the cooperative rearrangement of segments (motional units).5 Here, the size of the cooperatively rearranging region (CRR) ξ is a key parameter that characterizes segmental dynamics in supercooled liquids. The role of dynamic heterogeneity in segmental relaxation has also been investigated,3, 6 and the size of cooperativity ξ is often assumed to be directly connected to the length scale of the dynamic heterogeneity,1, 3, 7, 8 though the relation between these lengths is still subject to much discussion.9 Based on the concept of segmental rearrangement within the CRR, the number of segments per CRR NCRR is another essential parameter for characterizing the cooperative nature of segmental dynamics.5, 10 In this study, for the purpose of convenience, we define NCRR as the number of repeating units per CRR.

The drastic viscous slowdown leads to a non-Arrhenius behavior that is characterized by dynamic fragility parameter m defined as

where τ is α relaxation time and Tg is the glass transition temperature.11 The parameter m is closely related to the effective activation energy at Tg. The fragility m becomes greater as non-Arrhenius features become prominent. Many of the polymeric liquids are known to be fragile, that is, they exhibit relatively high values of m.11, 12 Experimental studies have revealed that both cooperativity and fragility depend significantly on polymer materials, that is, they are sensitive to detailed chemical structure.11, 12, 13 To elucidate the factors governing these parameters, it is essential to understand the mechanism behind viscous slowdown in polymer glass formers. It has been revealed that m depends on the rigidity of backbone chains relative to the side group.13 Hu et al.,14 on the other hand, proposed an empirical method to predict the value of m from the chemical structure of polymers. Furthermore, it is noteworthy that the fragility parameter plays an important role in determining the confinement effect on Tg.15, 16 This suggests that the origin of anomalous dynamics in nano-confined polymeric systems is intimately related to the material dependence of fragility.

The relationship between fragility and cooperativity has been a crucial issue in elucidating the nature of the viscous slowdown behavior. One could reasonably anticipate that fragile glass formers would exhibit high cooperativity. However, in general, no clear positive correlation between ξ and m was reported for a wide variety of polymers. Interestingly, a series of poly(n-alkyl methacrylate)s were found to show an apparent correlation between ξ(Tg) and m.17 In this system, the backbone chemical structure was the same and only the length of the end alkyl group was systematically varied. Considering such a result, the relation between cooperativity and fragility is expected to show a rather simple trend for polymeric systems possessing similar chemical structures.

In this study, we investigate the interrelation of glass transition temperature, fragility and cooperativity parameters on a series of polystyrene (PS) derivatives with various para-substituents. It has been reported that the position of the substitution in the phenyl unit affects the backbone dynamics, and that para-substitution exhibits the strongest effect on Tg in polychlorostyene.18 As these polymers possess an identical backbone structure, we expect a systematic trend between the glass transition parameters. We discuss how the observed correlations between the parameters should be interpreted based on the entropy-based relaxation model. For comparison, we also present the results of poly(methacrylic acid ester)s (PMAEs). These polymers also possess various substituents as the end ester parts but their backbone structure is the same.

To evaluate cooperativity in segmental dynamics, several techniques have been developed until now, including four-point dynamic susceptibility,2, 19, 20, 21 four-dimensional nuclear magnetic resonance,8, 21 boson peak spectroscopy7, 22, 23 and the calorimetric method.17, 19, 24, 25, 26 Among these, calorimetry is a notably useful technique that can provide information on both fragility and cooperativity. In particular, for the evaluation of fragility, calorimetry is one of the most favorable methods for determining m.16 Furthermore, recent developments in temperature-modulated differential scanning calorimetry (DSC) allow one to obtain a rather broad range of the heat capacity spectrum.26 Here we employ DSC as an effective tool for the evaluation of both fragility and cooperativity, also allowing us to compare literature data on PMAEs obtained by the same technique.17, 27

Experimental Procedure

The polymers used in this study are listed in Table 1. They were all purchased from Scientific Polymer Products (Ontario, NY, USA). The average molecular weights (Mn and Mw) were determined by size exclusion chromatography. The values of m reported in the literature tend to become scattered over wide ranges even for the same polymer material. For example, the reported values for atactic PS range from 80 to 180.11, 12 It has also been reported that m is quite sensitive to the evaluation method and, in some cases, to impurity (such as residual solvents) and to molecular weight.15, 16, 28 Regarding this point, we exercised additional caution: polymers were dissolved in benzene (1.0 wt%) and freeze-dried for 170 h to remove volatile impurities before use. Furthermore, for poly(ethyl methacrylate) (PEMA), poly(phenyl methacrylate) (PPhMA), poly(benzyl methacrylate) (PBzMA) and poly(cyclohexyl methacrylate) (PCHMA), purification by reprecipitation (three times, from tetrahydrofuran/n-hexane) was needed before the freeze–drying process to obtain reliable results. For stereoregular polymers (isotactic PS, syndiotactic PS, isotactic poly(methyl methacrylate) (PMMA), and syndiotactic PMMA), crystallinity may affect the segmental dynamics in the amorphous phase. To exclude such a crystallinity effect, the polymers were first heated to above their apparent melting temperature for 3 min, followed by quenching to room temperature to prevent crystallization. We confirmed that no signs of crystallinity were detected in a subsequent DSC heating scan.

Table 1 Parameters of polymers used in this study
Full size table

DSC measurements were performed using a Perkin Elmer (Waltham, MA, USA) Pyris Diamond calorimeter (power-compensation type) equipped with a Perkin Elmer Intra-cooler P2 cooling system. The temperature and heat flow were calibrated with an indium standard, and the measurements were performed in a nitrogen atmosphere. We used standard aluminum pans (Perkin Elmer 0219-0041) that were heated at 550 °C for 5 min just before use to remove any contaminants. Typical sample size ranged from 4 to 7 mg. Upon collecting DSC data for each sample, we first performed a scan on the above purified empty pan, and then we placed the specimen in the same pan and repeated the scan. The obtained trace was subtracted by that of the empty pan. This procedure greatly improved the accuracy and reproducibility of the data because the baseline of traces from the calorimeter of the power-compensation type often became unstable. To check the reproducibility of the data, iterative measurements for different specimens were performed several times for each material.

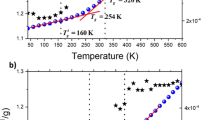
Fragility parameter m was evaluated based on the cooling rate dependence of fictive temperature Tf, based on the assumption that the Frenkel–Kobeko–Reiner constant is independent of the scanning rate.25 The polymer sample was first heated to Tg+50 K for 2 min, and was then cooled to Tg−50 K at cooling rate q that ranged from 1.0 to 20 K min−1. Finally, the sample was heated to Tg+50 K at 20 K min−1, and the obtained heating trace was analyzed to evaluate Tf.16, 29 Here we define Ts as a standard fictive temperature that was observed at a cooling rate qs=20.0 K min−1. From the slope of log (qs/q) vs Ts/Tf plot, we evaluated m. Figure 1 shows a typical example. In this paper, we also used the values of Ts as the (standard) glass transition temperature Tg for convenience, as listed in Table 1.

Figure 1
figure 1

Typical plot of log(qs/q) vs Ts/Tf for polystyrene. The solid line was obtained by linear regression analysis, and the fragility parameter m was evaluated from its slope.

Full size image

Cooperative length scale ξ at Tg can be estimated by the temperature-modulated DSC technique that provides complex heat capacity. In this study, we used an alternative simple method proposed by Donth et al.17, 30 The feasibility of this method is discussed elsewhere.17, 31 We performed step-scan heating measurements, a kind of temperature-modulated DSC:32 stepwise heating was executed, each step consisting of a heating period up to 2.0 K at a rate of 5.0 K min−1 and an isothermal period with a duration of <90 s. The temperature range of the step scan was from Tg−50 K to Tg+50 K. From the obtained reversing heat capacity traces, we evaluated the breadth of glass transition ΔT, defined as a temperature difference between the onset and endset of the transition. The temperature fluctuation parameter δT was estimated by using a relation δT=ΔT/C, where C is a constant. It should be noted that the breadth of glass transition on temperature scanning depends on the scanning rate.25 The mean heating rate of the step-scan was ∼2.3 K min−1 and was almost invariant for each scan, and we used an empirical value that C=5.0. We confirmed that the obtained δT values for PMAEs were consistent with values in the literature.17

To evaluate the cooperative length scale ξ(Tg), we used the following relation based on the fluctuation-dissipation theorem:17

with

where ρ is the mass density, k is the Boltzmann constant and CV(g) and CV(l) are the isochoric heat capacities at Tg in the glassy and liquid states, respectively. Isobaric heat capacities Cp(g) and Cp(l) at Tg were evaluated from the reversing heat capacity trace that was obtained by the step-scan measurement. Before the evaluation of the absolute reversing heat capacity, we performed a calibration with respect to a sapphire standard. The obtained values were further checked by comparing them with reported values if available.33 NCRR (Tg) was evaluated by

where ρn is the number density of segments, and we assumed d=3.

Wide-angle X-ray scattering (WAXS) measurements were performed using a Bruker (Billerica, MA, USA) AXS D8 Advance diffractometer with a Cu Kα generator operated at 40 kV and 40 mA. For measurements, polymer samples were melt pressed into a mold (trench) with a depth of 0.6 mm on a glass substrate. Line collimation was used, and 2θ/θ scan was performed through the use of a reflection mode. The raw scattering data were corrected for background scattering.

Results

We found that for the present PS derivatives, Tg becomes high as the bulkiness of the substituent increases (Table 1). Tg is the temperature at which the segmental relaxation time is comparable to the time constant of observation (typically 102–103 s), and may be mainly governed by the main chain stiffness and cohesive energy between segments.34 In the PS derivatives, the substituent is linked to the backbone chain via a relatively rigid phenylene unit, so that the substituent directly affects the mobility of the backbone chain dynamics. In contrast to the PS derivatives, Tg of PMAEs exhibits no clear trend with respect to the bulkiness of the ester (Table 1): the ester group is linked via a flexible -COO- linkage that makes the substituent effect indirect. Librational motion of phenyl group has been found to occur in polystyrene even at 200 K (far below Tg),35 suggesting that the phenylene units in the present PS derivatives have some degree of deformability around Tg. Nevertheless, phenylene unit is considered to be relatively rigid compared with the ester linkage in PMAEs.

The relation between m and Tg has been investigated for a wide variety of glass formers, and a positive correlation has been found regarding polymeric materials.36 This might be simply understood as meaning that less mobile (higher Tg) materials have greater activation energy. Indeed, it is derived from the Williams–Landel–Ferry relation that m is proportional to Tg and the apparent activation energy to Tg2.37 However, Agapov et al.37 reported that Tg is raised whereas m decreases when intermolecular interactions become stronger as in the case of poly(4-methylstyrene) and poly(4-chlorostyrene). Figure 2 shows a negative correlation for PS derivatives. This result implies that m tends to decrease as the bulkiness of the substituent increases. This may be understood by considering that cooperativity decreases as the bulkiness of the substituent increases. This point will be discussed later.

Figure 2
figure 2

Glass transition temperature Tg plotted against fragility m for (a) polystyrene derivatives and (b) poly(methacrylic acid ester)s. a-PMMA, atactic poly(methyl methacrylate); a-PS, atactic polystyrene; i-PMMA, isotactic poly(methyl methacrylate); i-PS, isotactic polystyrene; PBrS, poly(4-bromostyrene); PBzMA, poly(benzyl methacrylate); PCHMA, poly(cyclohexyl methacrylate); PClS, poly(4-chlorostyrene); PEMA, poly(ethyl methacrylate); PiPMA, poly(isopropyl methacrylate); PMOS, poly(4-methoxystyrene); PMS, poly(4-methylstyrene); PnBMA, poly(n-butyl methacrylate); PPhMA, poly(phenyl methacrylate); PsBMA, poly(sec-butyl methacrylate); PtBS, poly(4-tert-butylstyrene); s-PMMA, syndiotactic poly(methyl methacrylate); s-PS, syndiotactic polystyrene.

Full size image

On the other hand, just a very weak positive correlation is observed for PMAEs if we neglect the point for PPhMA. Such a correlation of PMAEs opposite to that of the PS derivatives seems to be interesting, but no systematic tendency with respect to the bulkiness of the ester part is found. In addition, the correlation is weaker than that for the PS derivatives: linear correlation coefficient r was estimated to be 0.622 if the data point of PPhMA is excluded, whereas r=−0.849 for the PS derivatives. These results suggest that variation of the ester part leads to different effects on the dynamics with respect to their chemical nature. Regarding this point, we infer that the ester part in PMAE can contact with various part of the polymer molecule (backbone and side group) because of the flexible -COO- linkage. Here we solely emphasize that the PS system exhibits rather simple and systematic trends for both Tg and m with respect to the substituent.

For PS derivatives, a distinct correlation between NCRR(Tg) and m was observed (Figure 3), whereas no apparent correlation was discernible for PMAEs. Linear correlation coefficient r was found to be 0.863 and 0.126 for the PS derivatives and PMAEs (neglecting PPhMA), respectively. A similar result was again observed in the plots of ξ3(Tg) vs m as shown in Figure 4. The results suggest that for PS derivatives, the effects of the substituent on Tg, m and the cooperativity parameters vary consistently, whereas for PMAEs the side group may affect the backbone chain dynamics in a rather complex manner, of which interpretation requires a more detailed consideration of the chemical structure. However, rather clear correlation is seen if the data points of PPhMA, isotactic PMMA and PBzMA are excluded. The open squares in Figure 3b are the literature values from Hemmpel et al.17 for PMAEs with n-alkyl esters. These data seems to be consistent with the present result, suggesting a positive correlation between cooperativity and fragility. The length of the linear alkyl group may cause the segmental dynamics to vary systematically.27 The other types of ester part such as benzyl and phenyl groups may affect the backbone dynamics in an appreciably different way from the linear alkyl groups, so that their data points are located far off the correlation line of the poly(n-alkyl methacrylate)s.

Figure 3
figure 3

Cooperativity parameter NCRR(Tg) plotted against fragility m for (a) polystyrene derivatives and (b) poly(methacrylic acid ester)s. The open squares represent data on poly(n-alkyl methacrylate)s from Hemmpel et al17 with alkyl group of 1: methyl, 2: ethyl, 3: propyl, 4: butyl, 5: pentyl and 6: hexyl. a-PMMA, atactic poly(methyl methacrylate); a-PS, atactic polystyrene; CRR, cooperatively rearranging region; i-PMMA, isotactic poly(methyl methacrylate); i-PS, isotactic polystyrene; PBrS, poly(4-bromostyrene); PBzMA, poly(benzyl methacrylate); PCHMA, poly(cyclohexyl methacrylate); PClS, poly(4-chlorostyrene); PEMA, poly(ethyl methacrylate); PiPMA, poly(isopropyl methacrylate); PMOS, poly(4-methoxystyrene); PMS, poly(4-methylstyrene); PnBMA, poly(n-butyl methacrylate); PPhMA, poly(phenyl methacrylate); PsBMA, poly(sec-butyl methacrylate); PtBS, poly(4-tert-butylstyrene); s-PMMA, syndiotactic poly(methyl methacrylate); s-PS, syndiotactic polystyrene.

Full size image
Figure 4
figure 4

Cooperatively rearranging volume ξ3(Tg) plotted against fragility m for (a) polystyrene derivatives and (b) poly(methacrylic acid ester)s. a-PMMA, atactic poly(methyl methacrylate); a-PS, atactic polystyrene; i-PMMA, isotactic poly(methyl methacrylate); i-PS, isotactic polystyrene; PBrS, poly(4-bromostyrene); PBzMA, poly(benzyl methacrylate); PCHMA, poly(cyclohexyl methacrylate); PClS, poly(4-chlorostyrene); PEMA, poly(ethyl methacrylate); PiPMA, poly(isopropyl methacrylate); PMOS, poly(4-methoxystyrene); PMS, poly(4-methylstyrene); PnBMA, poly(n-butyl methacrylate); PPhMA, poly(phenyl methacrylate); PsBMA, poly(sec-butyl methacrylate); PtBS, poly(4-tert-butylstyrene); s-PMMA, syndiotactic poly(methyl methacrylate); s-PS, syndiotactic polystyrene.

Full size image

The effects of stereoregularity on Tg, m and cooperativity were revealed to be insignificant for PS, though isotactic PS exhibits slightly greater fragility. On the other hand, isotactic PMMA exhibits a remarkably lower Tg and higher cooperativity than the other two PMMAs. The low Tg of isotactic PMMA is partially because of its low backbone stiffness as evidenced by the static stiffness parameter.38 It has been revealed that dynamic stiffness (segmental relaxation time) increases generally as static chain stiffness increases in dilute solutions.39, 40

Figure 5 shows the WAXS profiles for the present PS derivatives. It is known that polystyrene exhibits two dominant halos at around s=7.1 and 13.5 nm−1 (s=(4π/λ) sin θ).41, 42, 43 The lower s peak is called the polymerization peak because of its absence in the styrene monomer.41 In Figure 5, the lower s peak is clearly observed for atactic PS and poly(4-methylstyrene), whereas for the other PS derivatives the lower s peak is very weak. Table 3 shows locations and intensity ratio of the two major peaks: I1 and I2 are the peak intensities at s1 and s2, respectively. Here, the peak intensity was evaluated from an experimental polynomial for the peak region obtained by the nonlinear least squares fitting method.

Figure 5
figure 5

Wide-angle X-ray scattering profiles for the polystyrene (PS) derivatives. The scattering intensity is normalized with respect to the maximum peak height. a-PS, atactic polystyrene; PBrS, poly(4-bromostyrene); PClS, poly(4-chlorostyrene); PMOS, poly(4-methoxystyrene); PMS, poly(4-methylstyrene); PtBS, poly(4-tert-butylstyrene).

Full size image

Discussion

Correlation between cooperativity and fragility

According to the Adam–Gibbs theory,5 the segmental relaxation time τ(T) depends on both temperature and configurational entropy as

where Sc is the configurational entropy per segment, sc* the configurational entropy of the smallest CRR and Δμ the activation energy per segment. From the definition of m, we obtain

A positive correlation is expected from Equation (6) if Δμ/Tg does not depend on the material to a great degree, and this seems to be the case for the PS derivatives. This is reasonably understood by the higher barrier that has to be overcome for a larger (bulkier) substituent that simultaneously reduces the segmental mobility (Tg is raised), that is, both Δμ and Tg increase with an increase in the bulkiness of substituent. We estimated Δμ using Equation (6) as shown in Table 2. Calculation based on lattice cluster theory suggests that for a polymer with a flexible backbone, the stiffness of the side group raises Δμ/k,44, 45 consistent with the results shown in Table 2. Here, the value of Δμ varies quite reasonably with respect to the substituent bulkiness. An empirical relation Δμ/k=aTmc has been proposed, where Tmc is the experimental crossover temperature of the mode coupling theory46, 47, 48 with a=6–7.44, 49 If Tmc is largely proportional to Tg as predicted by the mode-coupling theory (Tmc=1.2 Tg), constancy of Δμ/Tg is derived.

Table 2 Activation energy per segment estimated from Equation (6)
Full size table

Structures in PS derivatives

As pointed above, the cooperativity parameter NCRR(Tg) for the PS derivatives decreases as the size of substituent becomes larger, implying that cooperative feature of segmental relaxation becomes prominent for the smallest substituent (−H), that is, polystyrene. We infer that this is relevant to the packing structure of the chains in an amorphous state. The lower s peak in the WAXS profile mainly reflects backbone–backbone correlation that has been assumed to be related to stacking of phenyl groups resulting in a superchain structure.43 The higher s peak, on the other hand, is the most intense one and mainly reflects phenyl–phenyl correlation. The existence of the polymerization peak suggests certain additional structural order in PS that may enhance the cooperativity in segmental rearrangement. One interesting feature is that the lower s peak increases with increasing temperature, whereas the higher s peak slightly decreases with increasing temperature. Interpretation of this behavior is rather complicated. Various types of atomic pairs, for example, backbone–backbone, phenyl–phenyl and backbone–phenyl atomic pairs, and also intra and inter-chain atomic pairs contribute to the two halos. Contribution of each type behaves in quite a different manner with temperature. Detailed discussion on this issue is made on the basis of simulation work.50, 51, 52, 53 We should also note that the lower s peak is sensitive to the packing structure as evidenced by the physical aging experiments.54

The result in Table 3 shows that I1/I2 becomes smaller as the substituent becomes bulkier. It is likely that the para-substituent weakens backbone–backbone correlation, leading to a reduction in segmental cooperativity. Bulky para-substituents probably prevent the stacking of phenyl groups that, as a result, reduces the strength of backbone–backbone correlation.

Table 3 Parameters estimated from WAXS profile
Full size table

The value of s1 tends to decrease with an increase in the substituent’s bulkiness (Table 3). This may be explained by an increase in the correlation distance between backbone chains when the substituent becomes larger. On the other hand, s2 is almost constant except for poly(4-tert-butylstyrene) (PtBS). This constancy may indicate that the phenyl–phenyl correlation is not perturbed significantly by the substituent even for -Br group. For PtBS, tert-butyl group occupies a large space than -Cl or -Br, and hence it may appreciably hinder the stacking structure of phenyl groups. The ratio of ξ(Tg) to phenyl–phenyl distance is estimated by ξ(Tg) s2/2π, as listed in Table 3. The obtained values lie within the range of various theoretical predictions of 3–6.7, 10, 20, 55 The tendency of substituent dependence of ξ(Tg) s2/2π seems to be a little different from that of I1/I2: poly(4-chlorostyrene) gives the lowest value for the former, whereas poly(4-bromostyrene) does so for the latter. This may reflect a fundamental difference in these parameters, that is, the cooperativity concerns dynamical phenomenon whereas WAXS characterizes static structural features.

Packing efficiency

It has been argued that fragility depends on the packing efficiency of the segments.44, 56 It may be intuitively understood that dense packing requires significant additional volume on rearrangement, leading to a high fragility (or a high barrier). Unfortunately, we found no clear correlation for m vs Vm, as well as for m vs ρ (mass density) for either the PS or PMAE systems (Table 1). Vm is a measure of segmental size, and ρ depends strongly on the elements included in the polymer. Neither of these may be an appropriate parameter for evaluating the packing efficiency. Recently, the pressure dependence of glass transition dynamics has been extensively investigated.57 It has been claimed that the activation volume, which practically determines the contribution of volume to fragility, should be correlated with cooperativity.7 In addition, a clear positive correlation has been revealed between the activation volume and ξ(Tg) for polymeric materials that have no similarity in chemical structure.23 The correlation between ξ3(Tg) and m observed for the present PS system suggests a dominant effect of the substituent's bulkiness on the dynamics rather than the cohesive energetic contribution from the para-substituent. We speculate that the isochoric part of the fragility plays merely a minor role in the dynamics of the PS derivatives.

The above consideration may be supported by values of the dipole moment μ0 of the monomer model compound shown in Table 1.58 Here μ0 may be a measure of nonbonded interactions between segments that are directly related to the cohesive energy between segments. If we assume that the degree of cooperativity in segmental relaxation is largely governed by the cohesive energy, we might expect a certain type of correlation to exist between NCRR(Tg) and μ0. However, we found no apparent correlation between the two parameters (Table 1). In particular, halogen-containing PS polymers show high μ0 values but low cooperativity. Thus, spatial hindrance due to the substituent is suggested to play a dominant role in the PS derivatives.

The packing efficiency may be related to the free volume in glassy materials. It has been pointed out that, in general, a material with lower fragility has less free volume.59 From the present data, the thermal expansion coefficient of the fractional free volume αf can be estimated by using a relation αf=k/Δμ.59 The result for the PS derivatives in Table 2 indicates that αf becomes smaller as m decreases. This might be consistent with the general trend of the correlation between free volume fraction and m.

Configurational entropy

It has been reported that for a large number of glass formers other than polymers, the configurational entropy of the smallest CRR, sc* depends on temperature, and a universal curve in the plot of sc* vs segmental relaxation time has been found.60 Although the temperature dependence of sc* is inconsistent with the assumption of the original Adam–Gibbs model,5 random first-order transition theory predicts that sc* increases with increasing temperature.22 The above universality implies that sc*(Tg) is almost invariant with respect to material. The value of sc*(Tg) may be ∼5–6 × 10−21 J K−1 for nonpolymeric glass formers.60 This may not be the case for polymeric materials because of the complex interactions between segments (including bonded and nonbonded interactions). However, from the obvious correlation between NCRR(Tg) and m observed for the present PS derivatives, we infer that sc*(Tg) does not vary significantly with respect to the substituent. In this case, the configurational entropy per segment Sc(Tg) (= sc*/NCRR(Tg)) is expected to increase as the substituent becomes bulkier. This point will be investigated in a forthcoming paper.

Conclusions

We investigated the glass transition temperature, fragility and cooperativity of PS derivatives possessing various para-substituents on the phenyl group. The following results were obtained: (1) glass transition temperature is raised consistently as the bulkiness of the para-substituent increases, (2) both cooperativity parameters, NCRR(Tg) and ξ3(Tg), exhibit a tendency to increase with increasing fragility and (3) both fragility and cooperativity tend to decrease as the substituent’s bulkiness increases. WAXS results suggested that the structural order that is responsible for the lower s peak is weakened by the bulkiness of the substituent, leading to the reduction of cooperativity in segmental dynamics. The systematic trends of glass transition dynamics seem to be characteristic to the present PS derivatives, where the substituent is attached to the backbone chain via phenyl ring. In this case, the origin of the substituent’s effects on the parameters may be rather simple because of the strong limitation of its spatial arrangement via phenyl group: the substituent plays a major role in changing the packing ability. Contrary to the PS system, PMAEs exhibit rather complex behaviors with less weaker correlations between the parameters. It is likely that the flexible ester linkage allows a variety of spatial arrangements of the substituent, leading to various types of segmental interaction.