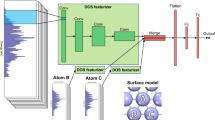
Abstract
Alloying has been proposed to circumvent scaling relations between the adsorption energies thus allowing for the complete optimization of multistep reactions. Herein the fidelity of scaling rules on high-entropy alloy (HEA) surfaces is assessed focusing on hydrogen-containing molecules, *AHx for A = C and N (x = 0, 1, 2, 3), A = S (x = 0, 1, 2) and A = O (x = 0, 1). Using an adsorbate- and site-specific deep learning model to rapidly compute the adsorption energies on CoMoFeNiCu HEA surfaces, the energies of *AHx and *A are shown to be linearly correlated if *A and *AHx have identical adsorption site symmetry. However, a local linear dependence emerges between the configuration-averaged adsorption energies irrespective of the site symmetry. Although these correlations represent a weaker form of the scaling relationships, they are sufficient to prohibit the optimization of multistep reactions. The underpinning of this behavior is twofold (1) the nearsightedness principle and (2) the narrow distribution of the adsorption energies around the mean-field value. While the nearsightedness is general for all electronic systems, the second criterion applies in HEAs with relatively strong reactive elements. The present findings strongly suggest that alloys may not generally enable the breaking of scaling relationships.
Similar content being viewed by others
Introduction
High-entropy alloy (HEA) nanoparticles bring exciting and yet unexplored opportunities for designing new catalysts with tailored properties. Notably, the carbothermal shock method1 allows for the incorporation of multiple metal elements into single-phase HEA nanoparticles. In addition, the recently-developed scalable aerosol synthesis2 method takes a further step toward producing HEA nanoparticles in bulk quantities with full potential for industrial use. Initial findings strongly suggest that HEA nanoparticles will constitute a paradigm shift in catalysis and energy applications by virtue of their heterogeneous surface chemistry that could simultaneously activate different reactions. In addition, the essentially countless number of HEA compositions could allow for the optimization toward the desired activity, selectivity, and stability3,4,5,6,7,8. However, this unlimited degree of tunability of HEA materials also challenges traditional approaches that rely on the “Edisonian” trial-and-error approach in the design of catalysts.
Computational approaches based on quantum mechanical density functional theory (DFT) are advantageous in the rational design of catalysts. Central to the success of these methods is their ability to easily compute the adsorption energy, i.e., interaction strength between adsorbates and catalytic surfaces. The adsorption energies can uncover the reaction mechanism and energetics at the molecular level9. In addition, developing the theory of catalysis, the so-called volcano relationship, that links the catalytic activity with adsorption energies and energies of reactions steps has empowered DFT with practical and efficient pathways for catalyst optimization10,11. However, despite the enormous methodological, hardware, and software innovations, it is still impractical for standard DFT approaches to characterize the adsorption strength of a relatively large number of different sites, which is required to yield an unbiased estimate of the catalytic activity. In this respect, alloys in general and particularly HEAs, represent a seminal challenge for standard DFT simulations12.
Machine learning (ML) approaches are revolutionizing many aspects of our life and their influence on materials modeling is becoming increasingly noticeable. For instance, ML enables significantly faster predictions of material properties than DFT methods, thus contributing to a paradigm shift in materials design where big data, artificial intelligence, and materials modeling are deeply entangled13,14,15,16,17,18,19. ML approaches have also been applied to compute the adsorption energy on metal surfaces yielding results that compare favorably with DFT calculations20,21,22,23,24,25,26,27. Rossmeisl and co-workers introduced an ML approach to computing the adsorption energy for HEA surfaces, which assumes that the energy is a linear function of the number of metal elements neighboring the adsorption site28,29. Also, in a recent study, Saidi and collaborators developed an ML model based on deep neural networks (DNN) to rapidly compute the adsorption energy for HEA surfaces. This DNN model showed high fidelity and was applied to optimize the composition of CoMoFeNiCu HEA catalysts toward ammonia synthesis and decomposition30. In addition, this study rationalized recent experimental results8, which demonstrated that the Co25Mo45Fe10Ni10Cu10 composition yields a high catalytic activity toward ammonia decomposition.
HEA surfaces require rethinking the tools and approaches developed for uniform surfaces31. Particularly, HEA surfaces are characterized by a spectrum of adsorption energies due to the enormous number of chemical environments that can be realized on the surface. Hence, it is not clear how to gauge their catalytic reactivity. Rossmeisl and collaborators introduced an exciting idea to assess surface reactivity based on the average adsorption energy that accounts for both the likelihood of realizing specific atomic arrangements on the surface, as well as their reactivity28. Thus, this probabilistic approach would ensure the high likelihood of having reactive sites on the surface. I posit that this concept of averaging is not new in catalysis. Nørskov and co-workers first introduced interpolation in the Periodic Table where bimetallic alloys on a volcano plot are located between the corresponding two constituent metals32, suggesting that the adsorption strength is averaged-out. However, I note as well that the “probabilistic” definition of the activity based on averaging is not consistent with the traditional approach that relies on the local geometry of reactive sites to define the surface catalytic activity. While recent studies have shown that the probabilistic approach can explain enhanced catalytic activities of complex alloys in agreement with experimental results29,30,33, more investigations are warranted to reconcile the ‘local geometry’ and the ‘probabilistic’ approaches for defining surface reactivity.
Scaling relationships between the adsorption energies of atoms and molecules are well known for metal surfaces and have been vital in the modern theory for catalyst design and optimization34,35,36,37,38,39,40,41,42. Ultimately such dependencies can be rationalized based on bond order conservation principles. Abild-Pedersen and collaborators used DFT to show that the adsorption energy ΔEx of *AHx (A = C, N, O, S with x = 0, 1, 2, 3) on different transition metal surfaces is linearly correlated with the corresponding adsorption energy of the central atom *A, irrespective of whether *A and *AHx have the same or different adsorption site symmetries43. These trends are derived based on the d-band model, which stipulates that ΔEx is proportional to \(V_{ad}^2\) where Vad is the Hamiltonian matrix element between the adsorbate and meta d states. The implications of these dependencies are multitude. First, these linear correlations, in addition to the Brønsted–Evans–Polanyi (BEP) relationship44 and the existence of competing rate-determining steps, explain the volcano relationship for hydrogenation and dehydrogenation reactions where the catalytic activity can be optimized using only the adsorption energy of the central atom43. For instance, in the case of ammonia synthesis and ammonia decomposition, nitrogen adsorption energy is a viable descriptor for catalyst optimization32,36,43,45,46. Also, from a practical point of view, these correlations are helpful for catalyst screening as only a single calculation is needed to uncover the adsorption energies of all intermediates. In addition, the scaling relations explain why it is challenging to fully optimize reactions with multiple intermediates because if the adsorption energy of one active site is optimized for one intermediate, it will negatively impact the stabilization of other intermediates.
The development of strategies to break scaling relationships is an active field of research in catalysis44,47,48. Notably, alloys even in the highly dilute bimetallic limit (single atom alloys) are proposed as an effective strategy for escaping the traditional scaling relationships, thus allowing for the complete optimization of multistep reactions31,44,49. For instance, a recent investigation on IrPdPtRhRu HEA surfaces by the Rossmeisl group reported a linear scaling relationship between *OH and *OOH but not between *O and *OH31. This breaking up of the scaling relationship between *O and *OH can be explained by differences in the adsorption site symmetries. Namely, both *OH and *OOH prefer on-top adsorption, making the scaling relationship between them universal irrespective of the surface composition. On the other hand, *O prefers to coordinate to three surface atoms in a hollow site that is different from the atop coordination of *OH, which breaks the correlations between the adsorption energies if the surface composition is not uniform31.
Herein I investigate the existence of scaling relationships in the adsorption energies of hydrogen-containing molecules on HEA surfaces focusing on CoMoFeNiCu HEA. Central to the present investigations is developing a high-fidelity DNN model that can resolve site-by-site the adsorption energy for *AHx on the HEA surface. I show that correlations between *A and *AHx adsorption energies only exist if *A and *AHx have identical adsorption site symmetry. Thus, CoMoFeNiCu breaks the universal scaling relationships, which hold on uniform metal surfaces where the correlations exist irrespective of the adsorption geometry. However, I show that a weaker form of the scaling relationship emerges between the configuration-averaged adsorption energies for a given HEA composition. I refer to these as local scaling relationships. Importantly, these local dependencies impose intrinsic limits on the tunability of the HEA composition toward optimizing a catalytic reaction, similar to the case of uniform metal surfaces. I posit that local scaling rules hold because of the nearsightedness principle and the narrow distribution of the adsorption energies around the mean-field value. While nearsightedness is a general principle for all quantum mechanical systems, the second requirement is in having strong adsorption centers in CoMoFeNiCu, namely Mo, Fe, Co, and Ni. I demonstrate that the local scaling relationships break in AgAuCuPdPt, which is characterized by nonreactive noble elements. Contrary to general beliefs, the present findings show that HEAs and likely other alloys cannot be generally used to break the scaling relationships to allow for the full optimization of multistep reactions.
Results and discussion
Development and validation of machine learning model for adsorption energies
I employ a slab approach with (111) fcc termination to investigate the interactions of *AHx with HEA surfaces. The DNN model for adsorption energies employs a convolutional neural network as done previously30. Briefly, the input layer of the convolutional network is passed to two convolutional layers, followed by one fully connected layer before passing to the output layer. The features associated with each adsorption energy encode the chemical environment of the adsorption site at four levels: (1) element-specific features that include ionization energy, electronegativity, electron affinity, and the number of valence electrons; (2) metal-specific features comprising of the Wigner-Seitz radius rs, d-band center ϵd, d-band filling fd, coupling matrix elements between adsorbate and metal d-states \(V_{ad},d\ln {\it{ \in }}_d/d\ln r_s\), and workfunction; (3) geometrical connectivity of the adsorption site; and (4) overall composition of the HEA.
The training set for the DNN model is generated from ~25 k DFT calculations of slab models with different chemical compositions and different adsorption sites. The size of the database employed for each model is shown in Supplementary Table 1. The initial adsorbate anchoring configurations on the surface are guided by the corresponding ones on pure surfaces and are somewhat justified from counting unsaturated bonds43. Namely, for *A and *AH (except *OH and *SH), the adsorbate attaches to the threefold hexagonal-closed pack (hcp) hollow site. The face-centered cubic (fcc) hollow site also has similar energy but is not investigated. The initial *AH2 position is at the bridge site with twofold coordination, while *AH3 and *OH are set at atop sites. Following structural optimizations, all adsorbate configurations retained mostly the initial symmetry. Because the DNN model is site-specific, I only included configurations with the same site symmetry in the training database.
Figure 1 shows a prediction parity plot for the *AHx adsorption energy obtained from the DNN model and conducted on a testing data set that was not included in the training and validation. The DNN model is trained on 80%, validated on 10%, and tested on the remaining 10% of the data set, all randomly chosen. Cross-validation is also performed by generating five unique models based on a different random selection of the training/validation/testing sets. For consistency, all adsorption energies are measured with respect to A2 (A = C, N, O, S) and H2 molecules. As seen from Fig. 1, the DNN values generally exhibit good agreement with the ground truth DFT energies where most of the DNN values fall within 0.1–0.2 eV from the reference values. This error is comparable to the intrinsic accuracy of the DFT approach employed to generate the training data set. Importantly, there is no systematic underestimation or overestimation of the DFT energies. The small value of the mean absolute error (MAE), shown as an inset in Fig. 1, also reflects the overall quality of the DNN predictions. The high fidelity of the DNN predictions further validates the convolutional neural network hyperparameters, training protocol, and the design of feature descriptors.
The adsorption site symmetry is color-coded as shown in the legend (top is light green, bridge is light blue, and hcp is light red). For each adsorbate, the upper inset in each subfigure shows the differences between the DNN and DFT values, and the lower inset shows the mean absolute error (MAE) for the overall accuracy of the model. All energies are in eV.
Assessing the validity of global linear scaling relationships
Using the DNN model, I next assess the fidelity of linear dependences in the adsorption energies. To this end, I have generated 2500 random slab configurations for 250 different alloy compositions to build a statistical ensemble that can capture trends in the adsorption energies. I verified that the findings are relatively similar using less/more (1500/5000) configurations. The HEA compositions were selected by uniformly varying the concentrations of the elements between 10% and 90%. I have verified that all of these compositions satisfy the empirical constraints for HEA stability namely, δr < 6.6% and \({{\Omega }} = \left( {T_m{{\Delta }}S_{{{{\mathrm{mix}}}}}} \right)/|{{\Delta }}H_{{{{\mathrm{mix}}}}}|\) > 1.1. Here δr is the difference in atomic radius, Tm the melting temperature, ΔSmix and ΔHmix the mixing entropy and enthalpy, respectively, and weighted averages are defined in terms of the concentration (ci) as \(\delta r = \mathop {\sum}\nolimits_{i,j}^k {c_ic_j\left( {r_i - r_j} \right){{\Delta }}H_{{{{\mathrm{mix}}}}}} = \mathop {\sum}\nolimits_{i,j}^k {c_ic_jH_{ij}T_m,{{\Delta }}S_{{{{\mathrm{mix}}}}}} = -\,k_B\mathop {\sum}\nolimits_i^k {c_i{{{\mathrm{ln}}}}c_i} ,\) and \(T_m\mathop {\sum}\nolimits_i^k {c_iT_{m \cdot }^i}\)50,51.
For *AHx that adapts a different site symmetry than the corresponding central atom *A, it is unclear how to correlate the energies given the surface heterogeneity. Herein, I choose to employ site-averaging over the three metal atoms located in the first nearest-neighbor shell of the hcp site. Namely, for the bridge (atop) symmetry, I average over the three different bridge (atop) sites associated with the hcp site. As can be seen in Supplementary Table 2 and Supplementary Fig. 1, the adsorption energies \(\Delta E^x\) for *AH (A = C and N) are found to correlate linearly with \(\Delta E^0\) of *A despite some scatter of the data. This is similar to the pure metal surfaces, and is also justified similarly considering that both *A and *AH occupy the same lattice site (hcp), and hence have the same chemical environment. On the other hand, the adsorption energies of *AH2 and *AH3 (as well as *OH and *SH), which have different adsorption site symmetry than *A, exhibit a significantly weaker or no correlation with *A adsorption energy.
The findings show that the scaling relationships in HEAs are not universal as in the case of metal surfaces, and only hold between adsorbates that have the same site symmetry. This finding is consistent with the breakup of the BEP relationship reported before on traditional alloyed surfaces44. The underpinning of this breakup is the heterogeneity of the surface that results in different chemical environments between adsorbates occupying different symmetry sties. Also, a similar breakup is reported for IrPdPtRhRu HEA31. Namely, it was found that the adsorption energies of *OH and *OOH are linearly correlated as both occupy the same atop configuration while as the scaling relationship between *OH and *O is no longer valid as *O occupies the hollow site that differs from that of *OH31.
Emergence of local linear scaling relationships
The absence of a universal linear correlation between adsorption energies of *A and *AHx that is site-independent suggests at first that HEA surfaces can, in principle, be utilized for the full optimization of multistep reactions31,52. However, I posit that this is not necessarily the case. While the HEA surface has a broad spectrum of adsorption energies that could be optimum for the intermediates, the corresponding configurations must be highly probable to maximize the catalytic activity28,29. Thus, in HEAs, and alloys in general, it is imperative to examine the average adsorption energy \(\widehat {\Delta E}\) rather than singling out the most optimum adsorption site. In the ensemble approach, \(\widehat {\Delta E}\) can be computed as \(\widehat {\Delta E} = {\sum }_\ell ^{n_s} f_\ell \Delta E_\ell / {\sum }_\ell ^{n_s} f_\ell\) where the summation is over a large number of random slab models (ns) with different atomic arrangements. For a given configuration, \(f = {\prod }_k^5 c_k^{N_k}\) counts the number of possibilities of generating a surface microstructure with Nk metal atoms consistent with HEA composition ck (dropped the configuration label l for clarity)28,29. The ensemble approach for computing \(\widehat {\Delta E}\) is equivalent to averaging over all different adsorption sites on a surface provided that the ensemble size is large enough (in practice, I found ns ~ 1000 to be sufficient). While the existence of linear correlations between \(\widehat {\Delta E}\) is a weaker form of the global scaling relationships between ∆E, these nevertheless could provide stringent conditions on the optimization of the HEA composition to maximize the reactivity toward a catalytic reaction28,29,30. I will refer to the correlations between \(\widehat {\Delta E}\) as local scaling relationships as these apply to energies associated with different alloy compositions regardless of the atomic arrangements.
I have computed \(\widehat {\Delta E}^x\) for *AHx using 250 different compositions of the CoMoFeNiCu HEA. This corresponds to ~1.2 × 106 configurations per intermediate, which is impractical to compute with standard DFT and is made possible thanks to the rapid computation of the adsorption energies using the DNN approach. As shown in Fig. 2a, there is a very strong linear correlation between \(\widehat {\Delta E}^x\left( {x\,>\, 0} \right)\) and \(\widehat {\Delta E}^0\) that is site-independent, similar to the case of pure metal systems43. This has two important implications. First, from a practical point of view, I only need to determine \(\widehat {\Delta E}^x\) for the central atom *A, and then I can use the scaling relationships to compute the average adsorption energies for *AHx. This would significantly save computational costs, thus alleviating the need to develop a DNN model for *AHx. Second, and most importantly, the local scaling relationships would suggest an intrinsic limit on optimally binding different intermediates simultaneously by tunning the HEA composition. Thus, similar to the pure metal surfaces, optimizing \(\widehat {\Delta E}^x\) for one intermediate, will concomitantly negatively impact the stabilization of other intermediates. These findings explain, in part, the recent experimental study, which showed that the adsorption energy of nitrogen is a good indicator of catalytic activity for CoMoFeNiCu HEAs toward ammonia decomposition8, as in the case of pure metals30. Moreover, the existence of local scaling relationships between *AHx and *A for A = C, N, O, and S strongly suggests that the adsorption energy of *A is a good indicator, at least for all hydrogenation and dehydrogenation catalytic reactions in the CoMoFeNiCu catalyst system.
Supplementary Table 3 summarizes the analysis of the linear fitting models. The quality of the fit can be assessed from the prediction parameter r2 reported in the table and from Fig. 2a. The intercept values depend trivially on the reference values that are chosen to compute the adsorption energy (here, I used the dimers A2 and H2). The fitting slopes for \(\widehat {\Delta E}^x\) vs. \(\widehat {\Delta E}^0\) depend on the number of the bonds between the surface and the adsorbate, decreasing as x increases43. This explains the weaker dependence of \(\widehat {\Delta E}^x\) on the alloy composition as x increases. For transition metal systems, it was shown based on the effective medium theory that \({{\Delta }}E^x = \gamma \left( x \right){{\Delta }}E^0 + \zeta \left( x \right)\) for \(x\,>\,0\) where the slope \(\gamma \left( x \right) = \left( {x_{{{{\mathrm{max}}}}} - x} \right)/x_{{{{\mathrm{max}}}}}\) with xmax = 4, 3, 2, and 2 for C, N, S, and O, respectively, is the maximum number of saturated bonds, and ζ(x) is the fitting intercept43. Comparing the slopes shown in Supplementary Table 3 for CoMoFeNiCu HEA to those of the transition metal surfaces in ref. 43, I note that the HEA values are larger and are generally in agreement for N, O, and S but less for C. It is not clear what is the underpinning for the differences. Notwithstanding, the trends found for CoMoFeNiCu HEA are on par with those for transition metal surfaces43. For instance, for C and N where there are more than two *AHx intermediates (xmax > 2), there is indeed a very high correlation between the slopes for CoMoFeNiCu and those for transition metal surfaces. In addition, as shown in Supplementary Table 3 the slopes for fitting \(\widehat {\Delta E}^1\)against \(\widehat {\Delta E}^0\)decreases along the sequence A = C, N, S, and O, also consistent with the behavior in transition metal surfaces43. In summary, the results show that CoMoFeNiCu behaves similarly to the uniform metal surfaces once the configuration-average \(\widehat {\Delta E}^x\) rather than microstate adsorption energy ∆Ex is considered in analyzing the correlations.
It is interesting to understand the underpinnings for the existence of the local linear scaling between \(\widehat {\Delta E}^x\) and corresponding \(\widehat {\Delta E}^0\) of the central atom. Such an understanding will determine whether these findings are transferable to other HEA systems. I hypothesize that these local dependencies are due to two main factors. First, the nearsightedness principle which stipulates that the adsorption energy tends toward the mean-field value where atoms coordinated with each nearest-neighbor tend to the average composition of the HEA28,29,30. As discussed in the introduction, this is consistent with the concept of interpolation in the Periodic Table proposed more than two decades ago32 to motivate finding optimum combination of metal atoms for catalytic applications. Second, the adsorption energies for a given chemical composition should have a narrow distribution around the mean-field value, as shown in Fig. 3a. See also Supplementary Table 6 that quantifies the dispersion of the adsorption energies using the interquartile (IQE) range. The nearsightedness in electronic matter is a general concept that applies to all quantum systems without long-range interactions53, e.g., nearsightedness explains Pauli’s concept of the chemical bond and the “divide and conquer” of Yang54. Hence, this requirement applies to all alloys. However, I posit that the small dispersion of the adsorption energies is not general to all alloy systems but is only associated with systems with strong adsorption centers. For instance, CoMoFeNiCu is characterized by highly reactive elements Mo, Fe, and to a lesser extent Co and Ni.
To further investigate the range of applicability of local scaling relationships in HEAs, I investigate AgAuCuPdPt that is characterized by noble and hence nonreactive elements. AgAuCuPdPt was investigated before for CO2 and CO reduction reactions29. Using the DNN approach, I develop a ML model for the adsorption energies ∆Ex for *AHx (A = C, N, O, S with x = 0, 1, 2, 3) to assess the correlations. As demonstrated in the parity plot of Supplementary Fig. 3, the DNN model has excellent predictivity of the adsorption energies. Comparing the distribution of the adsorption energies between CoMoFeNiCu (Fig. 1) and AgAuCuPdPt (Supplementary Fig. 3), I note that CoMoFeNiCu binds all adsorbates more strongly than AgAuCuPdPt. For instance, the medians of the adsorption energy reported in Supplementary Table 6 show that *C, *N, *O, and *S binds with −3.04, −0.81, −2.75, and −5.01 eV on CoMoFeNiCu while the corresponding values are −2.07, 1.5, −0.97, and −4.61 eV on AgAuCuPdPt. In addition to the appreciably weaker interactions between *AHx and the surfaces, the dispersion of the adsorption energies as quantified by IQR is also appreciably larger on AgAuCuPdPt compared to the corresponding values on CoMoFeNiCu. This is also apparent by inspecting Fig. 3. Both factors lead to a larger relative dispersion of the adsorption energies. Therefore, I do not expect the local scaling relationships to apply to AgAuCuPdPt. Figure 2, in addition to Supplementary Tables 4 and 5, shows that this is indeed the case.
In conclusion, I have examined the scaling relationships for hydrogen-containing molecules on HEA surfaces CoMoFeNiCu and AgAuCuPdPt. I show that these relationships are not universal as in the case of the uniform surfaces but only hold if *AHx occupies identical adsorption site as *A. Importantly, I show that local scaling relationships between the configuration-averaged adsorption energies hold irrespective of the site symmetry. Although these relations form a weaker form of the linear scaling between the adsorption energies, they are sufficient to show that CoMoFeNiCu cannot break the scaling relationships. The existence of these local dependencies is attributed to the nearsightedness principle for electronic interactions, and the existence of relatively strong adsorption sites in the HEA. In addition, I demonstrate that in AgAuCuPdPt, the local form of the scaling relationships holds less strongly than those in CoMoFeNiCu. The present study shows that HEAs and alloys cannot, in general, be used to circumvent the scaling relationships, as commonly believed31,44,49. More investigations are needed to fully understand the differences with pure metal surfaces. I argue that DFT accelerated with ML is viable for further investigations.
Methods
The DFT calculations are carried out using Vienna Ab initio Simulation Package (VASP) package, employing the Perdew–Burke–Ehrenzhof exchange-correlation functional55. I expanded the electronic wavefunctions using plane-waves with a 300 eV cutoff. Electron-nucleus interactions are modeled using projector augmented wave (PAW) pseudopotentials56,57. The slab fcc (111) models are represented using a 2 × 2 × 5 supercell. Finite-size effects with this supercell are expected to be small as demonstrated in a previous study for the adsorption of H and CO on two different HEA systems29. I sampled the Brillouin zone using a 3 × 3 × 1 shifted Monkhorst-Pack grid with 0.2 eV Gaussian smearing. All the atomic coordinates belonging to the top two layers of the slab and the adsorbates are optimized using 0.1 eV/Å force tolerance and with 10–5 eV energy tolerance to terminate the self-consistent electronic step. The computational setup including energy and force tolerances, in addition to the planewave cutoff has been verified to be adequate to yield converged adsorption energies up to ~0.1 eV. All CoMoFeNiCu calculations are performed with spin-polarized orbitals while AgAuCuPdPt systems are performed using spin-averaged calculations. Lattice constants of the HEAs are approximated as a weighted average based on the alloy composition, following Vegard’s law for binary alloys. This approximation was investigated recently and shown to possess the correct limiting behavior as the surface supercell size increases58. See also Supplementary Fig. 2. The convolutional neural network architecture is as described before19.
The adsorption energy ∆Ex for chemical species X is calculated as,
where \(E_X^ \ast\) is the energy of the relaxed slab with the adsorbed species, E* is the energy of the relaxed surface, and Eref is properly normalized energy measured with respect to H2 and A2.
Data availability
The data set used to train the convolutional neural network models will be shared with the community upon request.
References
Yao, Y. et al. Carbothermal shock synthesis of high-entropy-alloy nanoparticles. Science 359, 1489–1494 (2018).
Yang, Y. et al. Aerosol synthesis of high entropy alloy nanoparticles. Langmuir: ACS J. Surf. Colloids 36, 1985–1992 (2020).
Löffler, T. et al. Toward a paradigm shift in electrocatalysis using complex solid solution nanoparticles. ACS Energy Lett. 4, 1206–1214 (2019).
Löffler, T. et al. Discovery of a multinary noble metal-free oxygen reduction catalyst. Adv. Energy Mater. 8, 1802269 (2018).
Nellaiappan, S. et al. High-entropy alloys as catalysts for the CO2 and CO reduction reactions: experimental realization. ACS Catal. 10, 3658–3663 (2020).
Xin, Y. et al. High-entropy alloys as a platform for catalysis: progress, challenges, and opportunities. ACS Catal. 10, 11280–11306 (2020).
Amiri, A. & Shahbazian-Yassar, R. Recent progress of high-entropy materials for energy storage and conversion. J. Mater. Chem. A 9, 782–823 (2021).
Xie, P. et al. Highly efficient decomposition of ammonia using high-entropy alloy catalysts. Nat. Commun. 10, 4011 (2019).
Chen, B. W. J., Xu, L. & Mavrikakis, M. Computational methods in heterogeneous catalysis. Chem. Rev. https://doi.org/10.1021/acs.chemrev.0c01060 (2020).
Zhao, Z.-J. et al. Theory-guided design of catalytic materials using scaling relationships and reactivity descriptors. Nat. Rev. Mater. 4, 792–804 (2019).
Greeley, J. & Mavrikakis, M. Alloy catalysts designed from first principles. Nat. Mater. 3, 810 (2004).
Ferrari, A. et al. Frontiers in atomistic simulations of high entropy alloys. J. Appl. Phys. 128, 150901 (2020).
Pilania, G. et al. Machine learning bandgaps of double perovskites. Sci. Rep. 6, 19375 (2016).
Ward, L., Agrawal, A., Choudhary, A. & Wolverton, C. Ageneral-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2, 16028 (2016).
Weston, L. & Stampfl, C. Machine learning the band gap properties of kesterite I2-II-IV-V4 quaternary compounds for photovoltaics applications. Phys. Rev. Mater. 2, 085407 (2018).
Im, J. et al. Identifying Pb-free perovskites for solar cells by machine learning. npj Comput. Mater. 5, 37 (2019).
Jose, R. & Ramakrishna, S. Materials 4.0: materials big data enabled materials discovery. Appl. Mater. Today 10, 127–132 (2018).
Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O. & Walsh, A. Machine learning for molecular and materials science. Nature 559, 547–555 (2018).
Saidi, W. A., Shadid, W. & Castelli, I. E. Machine-learning structural and electronic properties of metal halide perovskites using a hierarchical convolutional neural network. npj Comput. Mater. 6, 36 (2020).
Andersen, M., Levchenko, S. V., Scheffler, M. & Reuter, K. Beyond scaling relations for the description of catalytic materials. ACS Catal. 9, 2752 (2019).
Mazheika, A. et al. Ab initio data-analytics study of carbon-dioxide activation on semiconductor oxide surfaces. Preprint at https://arxiv.org/abs/1912.06515 (2021).
Ghiringhelli, L. M., Vybiral, J., Levchenko, S. V., Draxl, C. & Scheffler, M. Big data of materials science: critical role of the descriptor. Phys. Rev. Lett. 114, 105503 (2015).
Ghiringhelli, L. M. et al. Learning physical descriptors for materials science by compressed sensing. N. J. Phys. 19, 023017 (2017).
Xin, H., Holewinski, A. & Linic, S. Predictive structure–reactivity models for rapid screening of Pt-based multimetallic electrocatalysts for the oxygen reduction reaction. ACS Catal. 2, 12–16 (2012).
Jäger, M. O. J., Morooka, E. V., Federici Canova, F., Himanen, L. & Foster, A. S. Machine learning hydrogen adsorption on nanoclusters through structural descriptors. npj Computat. Mater. 4, 37 (2018).
Li, Z., Wang, S., Chin, W. S., Achenie, L. E. & Xin, H. High-throughput screening of bimetallic catalysts enabled by machine learning. J. Mater. Chem. A 5, 24131 (2017).
Roling, L. T., Choksi, T. S. & Abild-Pedersen, F. A coordination-based model for transition metal alloy nanoparticles. Nanoscale 11, 4438–4452 (2019).
Batchelor, T. A. A. et al. High-entropy alloys as a discovery platform for electrocatalysis. Joule 3, 834 (2019).
Pedersen, J. K., Batchelor, T. A. A., Bagger, A. & Rossmeisl, J. High-entropy alloys as catalysts for the CO2 and CO Reduction Reactions. ACS Catal. 10, 2169–2176 (2020).
Saidi, W. A., Shadid, W. & Veser, G. Optimization of high-entropy alloy catalyst for ammonia decomposition and ammonia synthesis. J. Phys. Chem. Lett. 12, 5185–5192 (2021).
Pedersen, J. K., Batchelor, T. A. A., Yan, D., Skjegstad, L. E. J. & Rossmeisl, J. Surface electrocatalysis on high-entropy alloys. Curr. Opin. Electrochem. 26, 100651 (2021).
Jacobsen, C. J. H. et al. Catalyst design by interpolation in the periodic table: bimetallic ammonia synthesis catalysts. J. Am. Chem. Soc. 123, 8404–8405 (2001).
Saidi, W. A. Optimizing the catalytic activity of Pd-based multinary alloys toward oxygen reduction reaction. J. Phys. Chem. Lett. 13, 1042–1048 (2022).
Calle-Vallejo, F., Loffreda, D., Koper, M. T. M. & Sautet, P. Introducing structural sensitivity into adsorption–energy scaling relations by means of coordination numbers. Nat. Chem. 7, 403–410 (2015).
Greeley, J. Theoretical heterogeneous catalysis: scaling relationships and computational catalyst design. Annu. Rev. Chem. Biomolecular Eng. 7, 605–635 (2016).
Wang, S. et al. Universal transition state scaling relations for (de)hydrogenation over transition metals. Phys. Chem. Chem. Phys. 13, 20760–20765 (2011).
Zhao, Z. J. et al. Theory-guided design of catalytic materials using scaling relationships and reactivity descriptors. Nat. Rev. Mater. 4, 792 (2019).
Man, I. C. et al. Universality in oxygen evolution electrocatalysis on oxide surfaces. Chemcatchem 3, 1159–1165 (2011).
Nørskov, J. K. et al. Universality in heterogeneous catalysis. J. Catal. 209, 275–278 (2002).
Christensen, R., Hansen, H. A., Dickens, C. F., Nørskov, J. K. & Vegge, T. Functional independent scaling relation for ORR/OER catalysts. J. Phys. Chem. C. 120, 24910–24916 (2016).
Koper, M. T. M. Theory of multiple proton–electron transfer reactions and its implications for electrocatalysis. Chem. Sci. 4, 2710–2723 (2013).
Michaelides, A. et al. Identification of general linear relationships between activation energies and enthalpy changes for dissociation reactions at surfaces. J. Am. Chem. Soc. 125, 3704–3705 (2003).
Abild-Pedersen, F. et al. Scaling properties of adsorption energies for hydrogen-containing molecules on transition-metal surfaces. Phys. Rev. Lett. 99, 016105 (2007).
Darby, M. T., Stamatakis, M., Michaelides, A. & Sykes, E. C. H. Lonely atoms with special gifts: breaking linear scaling relationships in heterogeneous catalysis with single-atom alloys. J. Phys. Chem. Lett. 9, 5636–5646 (2018).
Vojvodic, A. et al. Exploring the limits: a low-pressure, low-temperature Haber–Bosch process. Chem. Phys. Lett. 598, 108–112 (2014).
Logadottir, A. et al. The Brønsted–Evans–Polanyi relation and the volcano plot for ammonia synthesis over transition metal catalysts. J. Catal. 197, 229–231 (2001).
Pérez-Ramírez, J. & López, N. Strategies to break linear scaling relationships. Nat. Catal. 2, 971–976 (2019).
Masa, J. & Schuhmann, W. Breaking scaling relations in electrocatalysis. J. Solid State Electrochem. 24, 2181–2182 (2020).
Kumar, G., Nikolla, E., Linic, S., Medlin, J. W. & Janik, M. J. Multicomponent catalysts: limitations and prospects. ACS Catal. 8, 3202–3208 (2018).
Yang, X. & Zhang, Y. Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 132, 233–238 (2012).
Zhang, Y. & Peng, W. J. Microstructural control and properties optimization of high-entrop alloys. Procedia Eng. 27, 1169–1178 (2012).
Chu, S. & Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 488, 294–303 (2012).
Kohn, W. Density functional and density matrix method scaling linearly with the number of atoms. Phys. Rev. Lett. 76, 3168–3171 (1996).
Prodan, E. & Kohn, W. Nearsightedness of electronic matter. Proc. Natl Acad. Sci. USA 102, 11635 (2005).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Clausen, C. M., Pedersen, J. K., Batchelor, T. A. A. & Rossmeisl, J. Lattice distortion releasing local surface strain on high-entropy alloys. Nano Res. https://doi.org/10.1007/s12274-021-3544-3 (2021).
Acknowledgements
The author is grateful for computing time provided in part by the Pittsburgh Center for Research Computing (CRC) resources a the University of Pittsburgh and Argonne Leadership Computing Facility, a DOE Office Science User Facility supported under Contract DE-AC02-06CH11357. This article was prepared as an account of work sponsored by an agency of the U.S. Government. Neither the U.S. Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the U.S. Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the U.S. Government or any agency hereof.
Author information
Authors and Affiliations
Contributions
W.A.S.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, and writing.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Saidi, W.A. Emergence of local scaling relations in adsorption energies on high-entropy alloys. npj Comput Mater 8, 86 (2022). https://doi.org/10.1038/s41524-022-00766-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-022-00766-y