Introduction

Materials with kagome lattice, composed of tiled corner-sharing triangles, have attracted enormous attention in recent decades due to its inherent geometrical frustration and strong correlations, inducing many exotic phenomena, such as spin liquid phase1,2,3, magnetic topological states4,5,6,7, chiral physics8,9,10, unconventional superconductivity8,9,11,12,13,14, etc. The genuine kagome materials host flat band in the entire Brillouin zone, Dirac point at K point and van Hove point (or saddle point) at M point. However, the relationship between the unique electronic structure and the corresponding exotic phenomena is still under hot debate for these kagome materials.

The V-based kagome metals AV3Sb5 (A = K, Rb, Cs) have been synthesized with a quasi-two-dimensional characteristic15. Subsequent studies have demonstrated that this family materials undergo the charge density wave (CDW) transitions in a temperature range form 80 to 102 K9,13,16,17,18,19,20. Further, this family materials also undergo the superconducting transitions at 0.93, 0.92 and 2.5 K for KV3Sb5, RbV3Sb5 and CsV3Sb59,13,14,15,16,17 respectively, and the superconducting transition temperature shows double-dome-liked pressure-dependent behavior under high pressure20,21,22. In addition, the nontrivial band characteristics are confirmed by angle resolved photoemission spectroscopy (ARPES), Shubnikov-de Haas oscillation measurements and theoretical calculations15,16,17,18,23. The coexistence of superconductivity and nontrivial band structures are necessary for the realization of topological superconductor and Majorana zero mode24,25. For example, the Majorana bound states have been experimentally detected in CsV3Sb513, where the Majorana bound states in the vortex core are proved to exist only with chiral p-wave pairing14.

Inspired by the fascinating properties of kagome metals AV3Sb5 (A = K, Rb, Cs), extensive experimental and computational works have been performed to design and synthesize novel kagome materials with an AV3Sb5-type isostructure. For examples, the high-throughput first-principles calculations are used to enlarge the family of AV3Sb5 prototype materials through element species substitution26,27,and the potential topological superconductivity and CDW orders are also predicted simultaneously27,28,29. Recently, the ATi3Bi5 (A = Cs, Rb) family materials have been experimentally synthesized30,31,32, which exhibit the orbital-selective nematic order30, nontrivial band topology31,32, superconducting transition with a critical temperature of 4.8 K30 and the pressure-induced double-dome superconductivity33. The fascinating electronic and transport properties of AV3Sb5 (A = K, Rb, Cs) and ATi3Bi5 (A = Cs, Rb) materials imply the necessity of theoretically designing other AV3Sb5 prototype structures and in-depth interpretation from electronic structure calculations, which could also supply more insights for exploring unconventional properties in various condensed systems.

In this work, we predict another family of kagome metals ANb3Bi5 (A = K, Rb, Cs) with the coexistence of superconductivity and non-trival band topology. The formation energy and phonon dispersion calculations demonstrate the relatively excellent thermodynamical and dynamical stabilities. Based on the Allen-Dynes-modified McMillan formula34,35, the superconducting transition temperatures for KNb3Bi5, RbNb3Bi5, and CsNb3Bi5 are predicted to be 2.11, 2.15 and 2.21 K, respectively. The calculated band structures without spin-orbit coupling (SOC) effect exhibit the characteristics of Dirac points, van Hove singularities and flat band in traditional kagome lattice. With SOC effect, the Dirac points are gapped, and all ANb3Bi5 (A = K, Rb, Cs) family materials are predicted as \({{\mathbb{Z}}}_{2}\)-topological metals. The coexistence of superconductivity and non-trivial band topology in ANb3Bi5 (A = K, Rb, Cs) family materials reported here will spark further experimental investigations.

Results and discussion

Crystal structure of ANb3Bi5

The ANb3Bi5 family materials crystallize in a layered hexagonal structure with the space group P6/mmm (No. 191), and can be constructed by partly element species substituting from AV3Sb5 or ATi3Bi5. As shown in Fig. 1, the ANb3Bi5 systems are formed by stacking Nb3Bi5 layers along c-axis via weak vdW interaction, where the alkali metal atoms can be regarded as inserted atoms between the Nb3Bi5 layers. The inserted alkali metal atoms are shown to play an important role in modulating the chemical potential, which means that the intercalation and deintercalation of alkali metal atoms will effectively shift the Fermi level without changing the dispersion of band structure15. The Bader charge analysis show the charge transfer effect in ANb3Bi5 (A = K, Rb, Cs) materials in Supplementary Table 1. One can see that each alkali metal atom transfer ~ 0.75 electron to the adjacent Nb3Bi5 layers, close to that of AV3Sb5 (A = K, Rb, Cs)15. In Nb-Bi slab, the Nb atoms form a net kagome lattice. The fully relaxed crystal structure parameters are listed in Table 1. One can see that the in-plane parameters have almost no change with increasing atomic number of alkali metal, while the lattice parameters along c-axis increase by ~ 0.29 Å from K to Cs, which is consistent with the previous high-throughput work26. It can be seen that our calculated lattice constants are slightly smaller than the high-throughput calculation results, and the vdW corrections included here give more accurate description of interlayer interactions. Furthermore, we compare the calculated parameters of CsNb3Bi5 with experimentally synthesized CsTi3Bi330, and the difference between them is rather small, demonstrating the reliability of our calculations.

Fig. 1: Crystal structure of ANb3Bi5 (A = K, Rb, Cs).
figure 1

a Side view of the crystal structure of ANb3Bi5. b Top view of the kagome layer. The green, blue, and orange balls indicate the alkali metal A (A = K, Rb, Cs), transition-metal Nb and Bi atoms, respectively.

Full size image
Table 1 Crystal parameters (in Å) and the formation energy (in meV) of ANb3Bi5 (A = K, Rb, Cs)
Full size table

Thermodynamic stability of ANb3Bi5

To evaluate the thermal stability of these components, we calculated the formation energy by

$${E}_{{{{\rm{formation}}}}}=\frac{{E}_{A{{{{\rm{Nb}}}}}_{3}{{{{\rm{Bi}}}}}_{5}}-{E}_{A}-3{E}_{{{{\rm{Nb}}}}}-5{E}_{{{{\rm{Bi}}}}}}{9}.$$
(1)

Here, \({E}_{A{{{{\rm{Nb}}}}}_{3}{{{{\rm{Bi}}}}}_{5}}\) is the total energy per formula cell. The EA, ENb and EBi are the energy per atom for alkali metal A (A = K, Rb, Cs), transition metal Nb and Bi elemental substances, respectively. The alkali metal A (A = K, Rb, Cs) and the transition metal Nb atoms crystallize in a body-centered cubic phase with the space group of \({Im \bar{3}m}\)36,37, while the Bi atoms exhibit the space group of \({R\bar{3}m}\)38. The calculated results in Table 1 show that the formation energies of these materials are all negative, demonstrating that ANb3Bi5 family materials are thermodynamically stable. This agrees well with the previous high-throughput work26, where the thermodynamic stability is evaluated by calculating the energy above hull. In addition, we also calculated formation energies with binary components as reactants in Supplementary Fig. 1. The results show that the ANb3Bi5 (A = K, Rb, Cs) family materials can be synthesized with their binary counterparts except for KBi2, RbBi2 and CsBi2.

Dynamic stability and Superconductivity of ANb3Bi5

Phonon dispersion is a key method to evaluate the dynamic stability of a system. The calculated phonon dispersions of ANb3Bi5 are shown in Fig. 2. One can see that there is no imaginary phonon mode for these three materials, indicating the structures are all dynamically stable. The maximums of phonon frequency are relatively close for these three materials. The phonon dispersion can be divided into two regions according to the vibration frequency. In the high-frequency region (ω > 125 cm−1), the phonons are composed of the vibration modes of Nb atoms. Comparing to the CsV3Sb5 and CsM3Te5 (M = Ti, Zr, Hf), the flat modes dominated by the out-of-plane vibration modes of the transition metals become more dispersive for ANb3Bi528,39. For the low-frequency region, the phonons are formed by mixing the vibrational modes of atoms alkali metal A (A = K, Rb, Cs) and Bi atoms. The K atoms have the smallest mass in KNb3Bi5, but the interaction between K atoms and Nb3Bi5 layers is relatively weak. Therefore, the K atoms exhibit the lower vibration frequency in Fig. 2a. This stronger localization for RbNb3Bi5 and CsNb3Bi5 in frequency space can be attributed to the fact that the less charge transfer from Rb/Cs atom and the enlargement of layer space make the interaction between alkali metal atoms and Nb3Bi5 layers weaker. When it comes to RbNb3Bi5 and CsNb3Bi5, the vibration modes hybridization gradually decreases and the vibration modes of Rb and Cs are more localized in frequency space. In addition, one can see that the lowest acoustic branch dominated by the out-of-plane vibrations of Bi atoms shows significant softening, which may induce larger electron-phonon coupling effect and a structural instability when the system temperature is down to a critical value, such as CDW transition. Therefore, we take the KNb3Bi5 as an example to check the temperature effect on phonon dispersion, and the phonon dispersion of KNb3Bi5 is recalculated via changing the Fermi-Dirac smearing factor σ. Here, σ corresponds to the electronic temperature of electronic subsystem40, and can be used to describe the CDW evaluation41,42. As shown in Supplementary Fig. 2, there is no imaginary modes for all calculated phonon dispersions, indicating that the system is stable under these temperatures and thus no CDW transition occurs.

Fig. 2: Phonon dispersions of ANb3Bi5 (A = K, Rb, Cs).
figure 2

Phonon dispersions weighted by different atomic vibrational modes of (a) KNb3Bi5, (b) RbNb3Bi5 and (c) CsNb3Bi5, respectively. The right panels of (a–c) are the total (gray-shaded zone) and vibrational mode-resolved (colored lines) phonon density of states (PhDOS). Phonon dispersions weighted by the magnitude of the phonon linewidth for (d) KNb3Bi5, (e) RbNb3Bi5, and (f) CsNb3Bi5, respectively. The right panels are the Eliashberg spectral function α2F(ω) (black line), and the integrated strength of electron-phonon coupling λ(ω) (red line).

Full size image

Encouraged by the discovery of superconductivity in AV3Sb5 (A = K, Rb, Cs) and ATi3Bi5 (A = Rb, Cs), a series of experimental and theoretical works have been performed to explore the other kagome-based superconducting materials, as listed in Supplementary Table 2. Here, we estimate the possible superconductivity in ANb3Bi5 family materials according to the Allen-Dynes modified McMillan formula34,35. The superconducting transition temperature Tc is calculated as

$${T}_{{{{\rm{c}}}}}=\frac{{\omega }_{\log }}{1.2}\exp \left(-\frac{1.04(1+\lambda )}{\lambda -{\mu }^{* }-0.62\lambda {\mu }^{* }}\right)$$
(2)

where the ωlog is logarithmically averaged characteristic phonon frequency, which is defined as

$${\omega }_{\log }=\exp \left(\frac{2}{\lambda }\int\frac{d\omega }{\omega }{\alpha }^{2}F(\omega )\log \omega \right).$$
(3)

The integrated electron-phonon coupling strength can be evaluated by

$$\lambda (\omega )\,{{\mbox{=}}}\,2\int\frac{{\alpha }^{2}F(\omega )}{\omega }d\omega .$$
(4)

The total electron-phonon coupling constant λ used in Eq. (2) is λ(ωmax), where ωmax is the maximum of the phonon frequency. The α2F(ω) mentioned above is the Eliashberg spectral function and can be calculated according to the following formula:

$${\alpha }^{2}F(\omega )=\frac{1}{2\pi N({E}_{F})}\sum\limits_{q\upsilon }\delta (\omega -{\omega }_{q\upsilon })\frac{{\gamma }_{q\upsilon }}{\hslash {\omega }_{q\upsilon }},$$
(5)

where ωqv are phonon frequencies, γqv is phonon linewidth as described by

$$\begin{array}{lll}{\gamma }_{qv}&=&2\pi {\omega }_{qv}\sum\limits_{ij}\int\frac{{d}^{3}k}{{\Omega }_{BZ}}{\left\vert {g}_{qv}(k,i,j)\right\vert }^{2}\\ &&\times \, \delta ({\varepsilon }_{q,i}-{\varepsilon }_{F})\delta ({\varepsilon }_{k+q,j}-{\varepsilon }_{F}).\end{array}$$
(6)

Here, the gqv(k, i, j) is the matrix of the electron phonon coupling and εq,i is the Kohn-Sham energy. The calculated Eliashberg spectral (black line) and integrated electron-phonon coupling strength (red line) are plotted in the right panel of Fig. 2d–f. Similar to CsM3Te5, the distributions of Eliashberg spectral function α2F(ω) are non-negligible at the high frequency region28. But for ANb3Bi5, the electron-phonon coupling from the high-frequency region (ω > 125 cm−1) reach 37 %, which can be attributed the soften modes around M/L points in ANb3Bi5. To explain this, we plotted the phonon dispersions weighted by the magnitude of the phonon linewidth (and consequently to the electron phonon coupling strength) in Fig. 2d–f. One can see that there are two obvious soften modes around M/L points. According to Eq. (4), these soften modes can induce stronger electron-phonon coupling effect. By comparing the phonon spectrum weighted by vibration modes of different atoms in Fig. 2a–c and weighted by the magnitude of the phonon linewidth in Fig. 2d–f, we can determine that the soften modes around M/L points result from the in-plane vibration modes of Nb-xy. In other words, the in-plane vibration modes of Nb have significant contribution to the electron-phonon coupling effect, as well as the superconductivity. For the lowest acoustic branch dominated by the out-of-plane vibrations of Bi atoms, the stronger electron-phonon coupling effect is clearly shown in Fig. 2d–f. The calculated total electron-phonon coupling constant λ are 0.548, 0.552 and 0.556 for KNb3Bi5, RbNb3Bi5 and CsNb3Bi5, respectively. Thus, this family materials can be classified as weak superconductors. The μ* in Eq. (2) is effective Coulomb pseudopotential, which has a significant impact on the value of Tc. We then check the influence of μ* on Tc. As shown in Supplementary Fig. 3, Tc decreases with increase of μ*. We used the value of μ* of 0.1 to calculate Tc in all calculations. The corresponding superconducting transition temperatures Tc at ambient pressure are 2.11, 2.15 and 2.21 K, slightly higher than these of CsTi3Bi5 (1.85 K) and RbTi3Bi5 (1.92 K)29. It is worth noting that both the electron-phonon coupling constant λ and superconducting transition temperatures Tc are very close for these three materials, which further confirms that superconductivity is attributed to the in-plane vibration modes of Nb-xy and out-of-plane vibrations of Bi-z.

Electronic structures and topological properties of ANb3Bi5

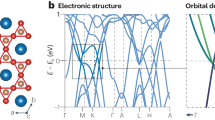
Without the SOC effect, the calculated band structures of ANb3Bi5 are shown in Fig. 3a–c. There are two bands crossing the Fermi level for both KNb3Bi5 and RbNb3Bi5, while there is only one band crossing the Fermi level for CsNb3Bi5. For the Nb-based kagome materials KNb3Bi5, there are two symmetry-protected Dirac points located at K (-0.605 eV) and H (-0.276 eV) points, which are dominated by the in-plane orbitals of Nb dxy/\({d}_{{x}^{2}-{y}^{2}}\). Considering that the inserted alkali metal A (A = K, Rb, Cs) plays an important role in charge transferring, the electronic structures near the Fermi level are barely changed by the removal of alkali metals16. We also calculated the band structure for the hypothetical compound Nb3Bi5 in Supplementary Fig. 4. It can be seen that the Dirac points are located at -0.141 eV, closer to the Fermi level. For ANb3Bi5, the band forming Dirac points also create four van Hove singularities (or saddle points) at M and L points. The two van Hove singularities with higher energy are mainly contributed by the orbitals of Nb \({d}_{{z}^{2}}\), while the lower two still result from the in-plane orbitals of Nb dxy/\({d}_{{x}^{2}-{y}^{2}}\). This orbital composition of Dirac points and van Hove singularities is consistent with these of CsV3Sb5 and CsTi3Bi531,39,43. The orbitals of Nb dxz/dyz contribute to several flat-band-liked bands along the whole high-symmetry path above the Fermi level (1.5 eV), while the orbitals of Nb dxy/\({d}_{{x}^{2}-{y}^{2}}\) create several partly flat bands along MKΓ and LH directions. The similar orbital characters of flat band were also reported for CsV3Sb543. Experimentally, the flat band, Dirac points and van Hove singularities are also partly observed in ARPES measurements of CsTi3Bi5 and CsV3Sb531,43. As is well-known, the electrons around the Fermi level have significant contribution to superconductivity. We can see that the density of states (DOS) at the Fermi level mainly result from the d orbitals of Nb atoms and p orbitals of Bi atoms. The orbital-resolved DOS are calculated to obtain accurate orbital distribution. The orbitals of Nb dxz/dyz and Bi px/py contribute the most to the DOS at the Fermi level. As shown in Fig. 3b–c, the characters of electronic structures of RbNb3Bi5 and CsNb3Bi5 are particularly similar to that of KNb3Bi5, demonstrating that the difference of superconducting transition temperature in these three materials can be rather small.

Fig. 3: Band structures without SOC for ANb3Bi5 (A = K, Rb, Cs).
figure 3

Orbital resolved band structure and density of states without the SOC effect for (a) KNb3Bi5, (b) RbNb3Bi5 and (c) CsNb3Bi5, respectively. The bands crossing the Fermi level are illustrated by the black line. The black and blue arrows are the Dirac points (DP) and van Hove singularities (vHs).

Full size image

For AV3Sb5 prototype kagome materials, the non-trivial topological properties are confirmed by theoretical calculations, ARPES and Shubnikov-de Haas oscillation experiments15,16,17,18,23. Here, we also investigate the topological properties via calculating the parity of the wave function at the time-reversal invariant momentum (TRIM) points and the surface states44. This method originates from the study of topological insulators, and recently it has been extended to the study of topological semimetals recently, such as YT6Sn6 (T = V, Nb, Ta)45, RV6Ge646, etc.

The calculated band structures with SOC effect for ANb3Bi5 are drawn in Fig. 4. Comparing to the band structures without SOC effect, the band structures change dramatically due to the large atomic mass. There is only one band crossing the Fermi level. For the bands around the Fermi level, the continuous band gaps are opened and plotted by the colored shadows in Fig. 4a–c. The Dirac-like bands crossing at K and H points are gapped by 0.239 and 0.168 eV for KNb3Bi5, 0.233 and 0.164 eV for RbNb3Bi5, 0.211 and 0.158 eV for CsNb3Bi5, respectively. One can see that the SOC-induced gaps are quite close for these three materials, similar to the case of AV3Sb5 (A = K, Rb, Cs)15. This can be attributed to the fact that the bands around the Fermi level exhibit similar orbital characteristics. The narrowest gaps, highlighted by the pink ellipses, are 6.2, 8.1 and 9.9 meV for KNb3Bi5, RbNb3Bi5 and CsNb3Bi5, respectively. Given that the systems hold both inversion and time-reversal symmetries, as well as the continuous band gaps across the whole BZ, we can calculate the \({{\mathbb{Z}}}_{2}\) indices of each band around the Fermi level via analyzing the parity of the wave function at the eight TRIM points23,28,39,45,46. The calculated results are listed in Table 2. For KNb3Bi5 and RbNb3Bi5, the non-trivial topological invariant \({{\mathbb{Z}}}_{2}\)= 1 can be assigned to band-I. Differently, both the band-I and band-III of CsNb3Bi5 exhibit non-trivial topological index. For the traditional hexagonal materials, there are two unequal surfaces28,45. Due to the vdW interaction between adjacent layers, the easiest cleavage surface is (001) surface. We investigate the surface state on the (001) surface. The calculated surface states for KNb3Bi5 are plotted in Fig. 5a. One can see that the surface states exist both above and below the Fermi level, where the one above the Fermi level are rather complicated. When we enlarge the part above the Fermi level (the skyblue dash area in Fig. 5a), we can see that there are four surface states and the SS3 and SS4 states cross at 0.325 eV, as shown in Fig. 5b. The isoenergy contour (E = 0.325 eV) along the whole BZ and enlarged around M point are calculated and presented in Fig. 5c–d. Experimentally, the surface states below the Fermi level can be detected by traditional ARPES with a higher binding energy or removal of alkali metals, while the one above the Fermi level needs time-resolved ARPES. The cases of RbNb3Bi5 and CsNb3Bi5 are very similar to KNb3Bi5, as shown in Supplementary Figures 5 and 6. Considering the non-trivial topological index and the surface states in ANb3Bi5 (A = K, Rb, Cs), we can define this family materials as \({{\mathbb{Z}}}_{2}\) topological metals.

Fig. 4: Band structures with SOC for ANb3Bi5 (A = K, Rb, Cs).
figure 4

Band structures with SOC effect for (a) KNb3Bi5, (b) RbNb3Bi5 and (c) CsNb3Bi5, respectively. The colored shadows illustrate the continuous band gaps along the whole high symmetry path. The pink ellipses indicate the minimum gap for each system.

Full size image
Table 2 Parity of wave function at TRIMs and the \({{\mathbb{Z}}}_{2}\) indices of ANb3Bi5 (A = K, Rb, Cs)
Full size table
Fig. 5: Surface states of KNb3Bi5.
figure 5

a Surface states of KNb3Bi5 along Γ-M-Γ direction. b Zoom-in surface states for the skyblue dash area in (a). Isoenergy contour (E = 0.325 eV) shows the green dash line in (b) along the whole BZ (c) and enlarged around M point (d).

Full size image

In summary, we have systematically investigated the coexistence of superconductivity and topological properties in the kagome metals of ANb3Bi5 (A = K, Rb, Cs). The lattice stability is confirmed by the calculations of formation energy and phonon dispersion. Based on the Allen-Dynes modified McMillan formula, the superconducting critical temperature are predicted to be 2.11, 2.15 and 2.21 K for KNb3Bi5, RbNb3Bi5, and CsNb3Bi5, respectively. For ANb3Bi5 (A = K, Rb, Cs), the superconducting transition temperatures are rather similar, which can be attributed to the similar contributions of vibration modes to electron-phonon coupling and electronic orbital to the DOS at the Fermi level. Without SOC effect, the Dirac-like band crossing points, van Hove singularities and the flat band are observed. Similar to the AV3Sb5 family materials, the non-trivial electronic structures are confirmed via analyzing the parity of the wave function around the Fermi level at the TRIM points and the surface states in (001) plane, demonstrating that all three materials can be categorized as \({{\mathbb{Z}}}_{2}\) topological metals. The coexistence of superconductivity and nontrivial band structures in ANb3Bi5 (A = K, Rb, Cs) may offer more opportunities for the synthesis of kagome materials and the exploration of complex interactions between superconductivity and non-trivial topological states.

Methods

First-principles calculations settings

The crystal structural optimization and electronic structure calculation were preformed via the Quantum ESPRESSO package based on density functional theory (DFT)47. The interaction between the electrons and ionic cores were described by ultrasoft pseudopotentials48, and the generalized gradient approximation (GGA) was used to treat the exchange-correlation interaction and parameterized by the Perdew-Burke-Ernzerhof functional49. Considering the quasi-two dimensional characteristic of crystal structures, the zero damping D3 van der Waals (vdW) correction was employed to describe the delicate vdW interaction between adjacent layers during crystal structural optimization50, which is proved to be reasonable while describing the isostructural AV3Sb5 family materials51,52. The cutoff energy of wave functions and charge density were set as 80 Ry and 800 Ry, respectively. The Gaussian smearing method was used with a smearing parameter of σ = 0.01 Ry to evaluate the charge density. The Brillouin zone (BZ) was sampled with a 16 × 16 × 12 k-points mesh for structural optimization, and all structures were fully relaxed until the force acting on each atom was <10−5 Ry/Å and the convergence threshold on total energy was set to be 10−6 Ry.

Phonon-related calculations

Phonon dispersion curves were calculated based on density functional perturbation theory (DFPT)53, where a denser 20 × 20 × 12 k-point grid and a 5 × 5 × 3 q-point grid were employed for the electron-phonon coupling calculations.

Surface states calculations

To investigate the projected surface states, we constructed a tight-binding model Hamiltonian by using maximally localized Wannier function (MLWF)54,55, where the s orbitals of alkali metal A (A = K, Rb, Cs), d orbitals of the transition metal Nb atoms and the p orbitals of Bi atoms were used as the basis set. Then, we used the iterative Greens function as implemented in WannierTools package and the constructed Hamiltonian to calculate the surface states related properties56,57.