Introduction

Warm/hot dense plasma exists widely in all types of stars1, the interior of giant planets2 and inertial confinement fusions3,4. Studies to these high-energy-density plasmas have been attracting wide attentions and extensive experiments have been made to explore their microscopic and macroscopic properties on large-scale scientific facilities of linac coherent light source (LCLS) X-ray laser5,6,7, national ignition facility (NIF)8 and Sandia Z facility9,10,11, etc. For atoms embedded in dense plasma, strong plasma screening effects are encountered due to complicated many-body interactions with the surrounding plasma, which significantly affects the atomic energy levels and wave functions, resulting in ionization potential depression (IPD), line shift, and remarkable changes in the photon, electron, and ion scattering cross sections12,13. In addition, the screening effects would further change the plasma properties simulation due to the basic atomic data applied in modeling plasma, such as the equation of state (EOS) and plasma spectra14,15, etc. Therefore, understanding the screening effects is essential for both fundamental researches and applications.

On the side of theory, various models have been developed to describe the plasma screening effects since the pioneering work of Debye and Hückel16, the well-known Debye–Hückel model was proposed in 1920s for non-degenerate and weakly coupled plasmas. Thomas–Fermi (TF) screening and self-consistent field ion-sphere (IS) models have been developed to treat the electron screening effects for degenerate plasmas17,18. Numbers of analytic models, such as the uniform electron gas model (UEGM)19, Ecker–Kröll (EK)20, Stewart–Pyatt (SP)21, and the models based on the analytic fits to IS potentials22,23,24, are proposed and widely used in the calculation of IPDs and line shifts in dense plasmas. Note that these models are developed based on the electron distribution from Boltzmann or Fermi–Dirac statistics, and their applications in treating hot dense plasmas are very limited due to the complicated many-body correlations involved in modeling dense plasma. The predictions from the above models have discrepancies to the spectra, line shifts, and IPDs in the latest high-precision spectra experiments of warm/hot dense plasmas5,6,7,25,26,27,28. Then, attempts for a better interpretation of the new measured IPD data have been made using different numerical and simulation methods, including Two-step Hartree–Fock (HF) calculations29, quantum statistical approach30,31, simulations based on the finite-temperature density functional theory32, and classical molecular dynamics simulations33.

On the side of the experiment, with the recent advances in obtaining a uniform, well-characterized, and high-energy-density plasmas, it becomes possible to precisely measure the ionic energy level shift in warm/hot dense plasmas5,25,26,27. The line-shift experiments are of high relevance to benchmarking electron screening models, since the line shift reflects the difference between the level shifts of two relevant energy states, which is very sensitive to the electron screening effects. Lately, Stillman et al.27 and Beiersdorfer et al.28 reported high-precision line-shift measurements of Al11+ and Cl15+ in hot-dense plasmas produced by high-intensity short-pulse lasers. They have used Li and Rosmej’s analytical model23 to calculate the line shifts but the results obviously deviate from the experimental ones. In order to resolve the discrepancies between measurements and calculations, quite a few simulations have been performed by using other models, including the numerical self-consistent field IS models34,35,36, the line-shift model based on SP screening potential37 and other analytical fits of IS models34,38,39. Unfortunately, these models only work for Cl15+ (1s3p−1s2) but fail for Al11+ (1s2p−1s2). In a word, the study of screening effects of warm/hot dense plasma presents still a largely unresolved problem, which is essentially determined by the many-body interactions between the specific ion and the plasma environment.

In this paper, a statistical electron screening model is proposed to describe the complicated many-body interactions of warm/hot dense plasmas. In this model, the collisions between plasma electrons and target ion, in particular, the most important three-body recombination processes strongly dependent on the state of the target ion, are taken into account in determining the electron distribution. Note that the target ion is used to represent the studied ion embedded in plasmas hereafter in the paper. This atomic-state-dependent screening model is validated by the line shifts of Al11+ (1s2p−1s2) and Cl15+ (1s3p−1s2) transitions in the latest experiments of Stillman et al.27 and Beiersdorfer et al.28, as well as the classical molecular dynamic simulations on the electron distribution of moderately coupled ultra-cold neutral plasmas (UNPs).

Results and discussion

Model formulation

In this work, the main goal is to treat the atomic structure of the atom/ion embedded in hot plasma. The present model is based on wave-function-based approach, in which the plasma field is usually represented as a screening model and the structure of target ion can be computed by solving Schrödinger or Dirac equation. The plasma-electron density distribution around the target ion in plasmas is the kernel of an electron screening model. This distribution is determined by all collision processes between electrons and the target ion.

The plasma-electron density of previous wave-function-based screening models, including Debye–Hückel, self-consistent field IS, UEGM, EK, and SP, is usually based on Fermi–Dirac distribution or Boltzmann distribution. For the electrons with Fermi–Dirac distribution

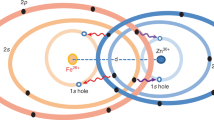
$$f_{{\mathrm{FD}}}\left( {p,{\boldsymbol{r}}} \right) = \frac{1}{{1 + \exp \left[ {\frac{1}{{k_{\mathrm{B}}T}}\left( {\frac{{p^2}}{{2m_{\mathrm{e}}}} - e{{\Phi }}\left( {\boldsymbol{r}} \right) - \mu } \right)} \right]}}$$
(1)

the number density of electrons is given by \(\rho _{{\mathrm{FD}}}\left( {\boldsymbol{r}} \right) = \frac{1}{{2\pi ^2\hbar ^3}}\int _0^\infty f_{{\mathrm{FD}}}\left( {p,{\boldsymbol{r}}} \right)p^2{\mathrm{d}}p\), where μ is the chemical potential, \({{\Phi }}\left( {\boldsymbol{r}} \right)\) is the total effective potential at position r, and p is the magnitude of electron momentum. In some popular wave-function-based screening models, such as the self-consistent field IS and SP, only contributions of free electrons are considered and \(p > p_0\left( {\vec r} \right) = \sqrt {2m_{\mathrm{e}}e{{\Phi }}\left( {\vec r} \right)} \) is applied to the Fermi–Dirac distribution to guarantee the electron energy to be positive18,19,20,21,22,23,24. However, in moderately/strongly coupled or dense plasmas with high-density free electrons, three-body recombination processes will happen significantly when the free electrons approach the target ion, and then affect the electron distribution of the target ion, as shown in Fig. 1. For the convenience of numerical calculation, the recombined bound electrons are usually treated as negative-energy ones with momentum \(p \,< \, p_0\left( {\vec r} \right)\).

Fig. 1: The scheme of a three-body recombination process.
figure 1

An electron transfers its energy and momentum to another free electron nearby and then recombines to the target ion with a specific bound state. Note that the recombined electron can produce a negative-energy electron around the target ion.

Full size image

The present model is proposed to extend these previous screening models by considering the contribution of negative-energy electron due to the inelastic collisions between target ion and plasma electrons. For weakly coupled plasmas, the mean kinetic energy of an electron is much larger than its mean potential energy and the free-electron distribution dominates the total electron density distribution. But for moderately/strongly coupled or dense plasmas, the distribution of negative-energy electron around the target ion is expected to deviate from equilibrium and play an important role in the total electron density distribution. In this case, the IPDs and line shifts of target ions will be impacted largely by the electron screening effects and cannot be accurately determined by the electron distribution of an equilibrium plasma consisting of free electrons, ions, and atoms. When taking into account the electron-screening effect on the \(nln\prime l\prime \) state of the target ion, the contribution of the \(nln\prime l\prime \) state and the transitions involved the \(nln\prime l\prime \) state should be excluded from the electron density distribution. In the case of Al11+ \(\left( {1s2p} \right)\), the contribution of the electrons recombined into \(1s2p(nl \cdots )\) states are considered in the present model, including

$$\begin{array}{*{20}{c}} {1s2p2s,\;1s2p^2,1s2p3s,\;1s2p3p,\;1s2p3d, \cdots } \\ {1s2p2s^2,\;1s2p^3,\;1s2p^22s, \cdots } \\ \cdots \end{array}$$
(2)

Therefore, the obtained negative-energy electron populations differ from the ones of the equilibrium model, which is the statistical average over all possible electron state populations.

Meanwhile, the laboratory plasmas are produced with intense ultrashort laser pulses and are non-equilibrium plasmas27,28. Therefore, in the present model, the negative-energy electron distribution is obtained through solving the rate equation. For simplicity, the plasma free electrons are assumed to be in equilibrium and the steady-state approximation is applied to obtain the distribution of negative-energy state for the given free-electron temperature and density. We consider a steady-state plasma with the number density \(n_{\mathrm{e}}\) of free electrons and the number density \(n_{{\mathrm{ion}}}\) of singly charged ions. The atom with a specifically bound state j can be formed through the three-body recombination of the target ion and its number density \(n_{{\mathrm{atom}}}^j\) can be determined by

$$\frac{{{\mathrm{d}}n_{{\mathrm{atom}}}^j}}{{{\mathrm{d}}t}} = \mathop {\sum }\limits_{j\prime } \left( {n_{\mathrm{e}}n_{{\mathrm{atom}}}^{j^\prime }K_{j^\prime j} - n_{\mathrm{e}}n_{{\mathrm{atom}}}^jK_{jj^\prime }} \right) - n_{\mathrm{e}}n_{{\mathrm{atom}}}^j\alpha _j + n_{\mathrm{e}}^2n_{{\mathrm{ion}}}\beta _j = 0.$$
(3)

Here, \(\alpha _j\) and \(\beta _j\) are the rate coefficients of electron collision ionization and three-body recombination, \(K_{j^\prime j}\) and \(K_{jj^\prime }\) are the rate coefficients of excitation and de-excitation, respectively.

In order to describe the non-equilibrium feature of plasma-electron distribution around the target ion, we defined a non-equilibrium coefficient \(\chi ^j\) and \(n_{{\mathrm{atom}}}^j = \chi ^jn_{{\mathrm{atom}},{\mathrm{equil}}}^j\). Here \(n_{{\mathrm{atom}},{\mathrm{equil}}}^j\) is the population density for an equilibrium system with the same number densities of \(n_{\mathrm{e}}\) and \(n_{{\mathrm{ion}}}\) can be calculated by using Fermi–Dirac statistics. Combining the classical scattering and equilibrium distribution, the non-equilibrium coefficient is given by

$$\chi \left( {{\boldsymbol{p}},{\boldsymbol{r}}} \right) = 2\sqrt {\varepsilon _{\mathrm{r}}/(\pi k_{\mathrm{B}}T)} \exp [ - \varepsilon _{\mathrm{r}}/(k_{\mathrm{B}}T)]/{\mathrm{Erf}}\left( {\sqrt {\varepsilon _{\mathrm{r}}/(k_{\mathrm{B}}T)} } \right),$$
(4)

where \({\mathrm{Erf}}\left( x \right)\) is the error function and \(\varepsilon _r = e{{\Phi }}\left( {\boldsymbol{r}} \right) - p^2/2m_{\mathrm{e}}\) is the absolute energy of the negative-energy electron. The details of the deviation of Eq. (4) are presented in Supplementary Note 1.

With the non-equilibrium coefficient \(\chi \left( {{\boldsymbol{p}},{\boldsymbol{r}}} \right)\) obtained, the negative-energy density distribution can be calculated with \(f_{{\mathrm{FD}}}\left( {{\boldsymbol{p}},{\boldsymbol{r}}} \right)\chi \left( {{\boldsymbol{p}},{\boldsymbol{r}}} \right)\), and the total plasma-electron density is given by

$$\rho \left( {\boldsymbol{r}} \right) = \frac{1}{{2\pi ^2\hbar ^3}}\left[ {\int _0^{p_0} f_{{\mathrm{FD}}}\left( {p,{\boldsymbol{r}}} \right)\chi \left( {p,{\boldsymbol{r}}} \right)p^2{\mathrm{d}}p + \int _{p_0}^\infty f_{{\mathrm{FD}}}\left( {p,{\boldsymbol{r}}} \right)p^2{\mathrm{d}}p} \right].$$
(5)

Due to the degeneracy effect (i.e., the Pauli exclusive principle) between the recombined and initially bound electrons, the recombined electron prefers to populate the outer orbital unoccupied. Therefore, the integration limit of the first term of Eq. (5) should be changed and the plasma-electron density around the target ions within a specific bound state can be obtained

$$\rho \left( {\boldsymbol{r}} \right) = \frac{1}{{2\pi ^2\hbar ^3}}\left[ {\int _{\sqrt {2m_e(\varepsilon _{\mathrm{b}} - e{{\Phi }}\left( {\boldsymbol{r}} \right))} }^{p_0} f_{{\mathrm{FD}}}\left( {p,{\boldsymbol{r}}} \right)\chi \left( {p,{\boldsymbol{r}}} \right)p^2{\mathrm{d}}p + \int _{p_0}^\infty f_{{\mathrm{FD}}}\left( {p,{\boldsymbol{r}}} \right)p^2{\mathrm{d}}p} \right],$$
(6)

In Eq. (6), the momentum p of the negative-energy electron is larger than \(\sqrt {2m_{\mathrm{e}}(\varepsilon _{\mathrm{b}} - e{{\Phi }}\left( {\boldsymbol{r}} \right))} \), where \(\varepsilon _{\mathrm{b}}\) is the energy of the outermost bound electron and its value will significantly affect the negative-energy electron distribution of the target ion.

The total effective potential \({{\Phi }}({\boldsymbol{r}})\) of the target ion can be obtained from

$${{\Phi }}\left( {\boldsymbol{r}} \right) = {\int} {\frac{1}{{4\pi \varepsilon _0\left| {{\boldsymbol{r}} - {\boldsymbol{r}}^\prime } \right|}}\left[ {Ze\delta \left( {{\boldsymbol{r}}^\prime } \right) - e\rho _{\mathrm{b}}\left( {{\boldsymbol{r}}^\prime } \right) - e\delta \rho ({\boldsymbol{r}}^\prime )} \right]{\mathrm{d}}{\boldsymbol{r}},}$$
(7)

where \(\delta \rho \left( {\boldsymbol{r}} \right) = \rho \left( {\boldsymbol{r}} \right) - \rho _{\mathrm{e}}\) is the plasma-electron density fluctuation induced by the presence of the target ion, \(\rho _{\mathrm{e}}\) is the mean free-electron density, \(\rho _{\mathrm{b}}\left( {\boldsymbol{r}} \right)\) is the density of initially bound electrons, and can be calculated by using multi-configuration Dirac–Fock approach40,41. It can be found that \({{\Phi }}({\boldsymbol{r}})\) and \(\delta \rho \left( {\boldsymbol{r}} \right)\) in Eq. (7) are dependent on each other and can be calculated with an iteration approach (see the “Methods” section).

In Fig. 2, we show the electron densities \(\rho \left( {\boldsymbol{r}} \right)/\rho _{\mathrm{e}}\) obtained from the present model together with those from Debye–Hückel model and IS model at the position r with \({{\Phi }}\left( {\boldsymbol{r}} \right) = 1/(4\pi \varepsilon _0a_{{\mathrm{WS}}})\), where \(a_{{\mathrm{WS}}}\) is the Wigner–Seitz radius. As well known, the Debye–Hückel and ion sphere screening models are only valid under the weak-coupling and strongly degeneracy limit conditions, respectively. As shown in Fig. 2, the present model converges to Debye–Hückel model and IS model (corresponding to the free-electron distribution) at the corresponding plasma conditions. This indicates that the present model is more accurate and provides a unified framework for the electron screening of plasmas with wide range of temperatures and densities.

Fig. 2: Comparison of plasma electron density between different models.
figure 2

The electron densities \(\rho \left( {\boldsymbol{r}} \right)/\rho _{\mathrm{e}}\) at the position r with \({{\Phi }}\left( {\boldsymbol{r}} \right) = 1/(4\pi \varepsilon _0a_{{\mathrm{WS}}})\) with different temperatures and densities. a The electron densities \(\rho \left( {\boldsymbol{r}} \right)/\rho _{\mathrm{e}}\) are shown as a function of temperature Te with the fixed mean electron density being \(\rho _{\mathrm{e}} = 1 \times 10^{22}{\mathrm{cm}}^{ - 3}\). b The electron densities \(\rho \left( {\boldsymbol{r}} \right)/\rho _{\mathrm{e}}\) are shown as a function of \(\rho _{\mathrm{e}}\) with the fixed temperature \(T_{\mathrm{e}} = 10\;{\mathrm{eV}}\). The solid lines are the results of the present model and the ones of Debye–Hückel and ion-sphere models are shown in dash line and short dash line, respectively.

Full size image

Line-shift calculation

For demonstration, we apply the model to the computation of the line shifts (see the “Methods” section) in the latest experiments27,28. In the experiments, the laser-produced hot-dense and weakly coupled non-equilibrium plasmas with (ρe, Te) = (1–5 × 1023 cm−3, 250–375 eV) for Al11+ 27 and (ρe, Te) = (3–6 × 1 023 cm−3, 600–650 eV) for Cl15+28, respectively. The Coulomb coupling parameters \(\Gamma _{\mathrm{e}} = e^2/(4\pi \varepsilon _0a_{{\mathrm{WS}}}k_{\mathrm{B}}T_{\mathrm{e}})\) are about 0.03–0.07, the charge state number Q of Al11+and Cl15+ are 11 and 15, respectively. We first compute, using the present model, the electron distribution fluctuations \(\delta \rho ({\boldsymbol{r}})\) of Al11+ and Cl15+ as well as a single-charged target ion with Q = 1 for comparison, for \(\rho _{\mathrm{e}} = 3 \times 10^{23}{\mathrm{cm}}^{ - 3},\,T_{\mathrm{e}} = 300\,{\mathrm{eV}}\,{\mathrm{and}}\,\Gamma _{\mathrm{e}} = 0.052\). The results are shown in Fig. 3a together with those from other models. It is shown that for the case of Q = 1, the present results are consistent with the results of Fermi–Dirac distribution. However, for the cases of Al11+(Q = 11), present results are very different from those of Fermi–Dirac distribution as shown in Fig. 3b. This indicates that \({{\Gamma }}_{\mathrm{e}}\) is independent of the Q, whereas the electron distribution around the target ion is sensitive to the ratio of the potential and kinetic energy of the electron, which can be approximated by \(e{{\Phi }}\left( r \right)/k_{\mathrm{B}}T \approx Qe^2/(4\pi \varepsilon _0{\boldsymbol{r}}k_{\mathrm{B}}T)\). In the present case of Q = 1,\(e{{\Phi }}\left( r \right) \,< \,k_{\mathrm{B}}T\) and the electron distribution of the present model is very close to the Fermi–Dirac one. While in the present case of Q = 11 and 15, \(e{{\Phi }}\left( r \right) \,> \,k_{\mathrm{B}}T\) and the negative-energy electron distribution is quite different from the Fermi–Dirac one due to the contribution of three-body recombination processes, see Supplementary Discussion for details. Thus, for moderately/strongly coupled or dense plasmas with \(e{{\Phi }}\left( r \right) \,> \, k_{\mathrm{B}}T\), the contribution of three-body recombination processes becomes important and should be included in the calculation.

Fig. 3: Electron density fluctuations of ion embedded in hot dense plasma.
figure 3

a, b Electron density fluctuations \(\delta \rho (r)\) versus r obtained from the present model and other models for the charge state numbers of a Q = 1 and b Q = 11 (Al11+). The mean electron density \(\rho _{\mathrm{e}}\;{\mathrm{is}}\;3 \times 10^{23}{\mathrm{cm}}^{ - 3}\), the temperature \(T_{\mathrm{e}}\;{\mathrm{is}}\;300\;{\mathrm{eV}}\). The distance r ranges from 0 to \(a_{{\mathrm{WS}}}/2 \approx 0.88\). Electron densities from Fermi–Dirac distribution (dash line), linear Debye–Hückel model (dot line) and the present model (solid line) are shown in panels a and b. In panel b, the present model with the condition of \(\varepsilon _{\mathrm{p}} \,> \,\varepsilon _{2p}\) and \(\varepsilon _{\mathrm{p}} \,> \,\varepsilon _{3p}\) are shown in dash–dot–dot line and dash-dot line, respectively. Here, \(\varepsilon _{\mathrm{p}}\) is the energy of recombined electron, \(\varepsilon _{2p}\) and \(\varepsilon _{3p}\) are the orbital energies of 2p and 3p, which are about −498 and −217 eV, respectively.

Full size image

By using the plasma-electron density fluctuation \(\delta \rho (r)\), the line shifts of Al11+ (1s2p−1s2) and Cl15+ (1s3p−1s2) are computed (see the “Methods” section). The results are shown in Fig. 4 together with the experimental results27,28 and the results from the numerical calculations of multi-configuration-Dirac–Fock self-consistent finite-temperature IS model (MCDF-SCFTIS)34 and the average-atom IS model (AA-IS)35,36. It is shown that the present results are in very good agreement with the experimental results for both Al11+and Cl15+. The results of MCDF-SCFTIS and AA-IS models are in good agreement with the experimental results for Cl15+ (1s3p−1s2) but are obviously underestimated for Al11+ (1s2p−1s2). Recently, Li and Rosmej34 proposed an analytical b-potential approach based on the MCDF-SCFTIS model, in which one adjustable parameter b was introduced to characterize the plasma-electron density. In order to get the results agreed with the experimental results, b = 4 and b = 2 are applied to the calculations for Al11+ (1s2p−1s2) and Cl15+ (1s3p−1s2), respectively. Whereas, as discussed below, the present model does not need any adjustable parameter although the plasma screening effects are dependent on the specific bound state considered.

Fig. 4: Line-shift results comparison.
figure 4

a, b The comparison of line shifts from experiments and different calculations for a 1s2p−1s2 transition in Al11+ and b 1s3p−1s2 transition in Cl15+. The dots are the experimental data, and the error bars are the uncertainties of the measurements27,28. The theoretical line-shift results are obtained by using the present screening model (solid line), MCDF-SCFTIS34 (dash line with squares), and AA-IS models35,36 (dash line with triangles).

Full size image

From the atomic-physic view of point, there are three kinds of interaction/correlation in plasma: the one between free electrons, the one between free electron and ion (bound electron), and the one between ion and ion. In order to consider the correlations between free electron and ion, the present model include the contribution of negative-energy electron through considering the three-body recombination process between target ion and plasma electrons. As shown in Eq. (6), the negative-energy electron density is state-dependent on the target ions studied since that a condition of \(\varepsilon _{\mathrm{p}} \,> \,\varepsilon _{\mathrm{b}}\) is used to guarantee the quantum degeneracy between the initial and recombined bound electrons, where \(\varepsilon _{\mathrm{p}}\) is the energy of recombined electron and \(\varepsilon _{\mathrm{b}}\) is the initial outermost orbital energy. In the calculations of the line shifts, \(\varepsilon _{\mathrm{p}} \;> \; \varepsilon _{3p}\) and \(\varepsilon _{\mathrm{p}} \,> \,\varepsilon _{2p}\) are applied for Cl15+ (1s3p−1s2) and Al11+ (1s2p−1s2), respectively. In order to gain insight into the dependence of plasma-electron density on \(\varepsilon _{\mathrm{b}}\), the electron density fluctuations \(\delta \rho \left( r \right)\) of Al11+ ion are computed and shown in Fig. 3b for different energies (\(\varepsilon _{2p}\) and \(\varepsilon _{3p}\)). It is found that the \(\delta \rho \left( r \right)\) of \(\varepsilon _{2p}\) is significantly larger than the one of \(\varepsilon _{3p}\). This indicates that the plasma-electron density distribution is sensitive to the specific bound state studied, which has also been verified by the good agreements with line-shift experiments27,28.

Validation

The calculated electron density distributions of the target ions depend on the models used. For further validation of the present model, we performed CMD simulations to the electron density distribution around the target ion of UNPs because it is a good prototype to study the many-body effects of moderately coupled plasmas using the CMD method. As pointed by Bergeson et al. in their review paper42, UNPs display the physics of strongly coupled and moderately shielded plasmas without quantum degeneracy. The details of the CMD simulations are provided in Supplementary Note 2. The obtained CMD results of electron density fluctuation \(\delta \rho \left( r \right)\) are presented in Fig. 5 together with those of Fermi–Dirac distribution and Debye–Hückel model for (a) \(\,\rho _{\mathrm{e}} = 10^9{\mathrm{cm}}^{ - 3},\,T_{\mathrm{e}} = 5.5{\mathrm{K}},\Gamma _{\mathrm{e}} = 0.49\) and (b) \(\rho _{\mathrm{e}} = 10^9\,{\mathrm{cm}}^{ - 3},\,T_{\mathrm{e}} = 11.5{\mathrm{K}},\Gamma _{\mathrm{e}} = 0.23\). It is shown that the results of the present model are in very good agreement with those of CMD simulations, while the results of the other two models apparently deviate from those of CMD simulations. The model of the Fermi–Dirac distribution obviously overestimates the plasma-electron densities near the target ion, indicating the non-equilibrium feature of the electron distributions. In Debye–Hückel model, the electron density distribution \(\rho \left( r \right) = \rho _0[1 + e{{\Phi }}(r)/(k_{\mathrm{B}}T)]\) used is a linear approximation of the Boltzmann distribution \(\rho \left( r \right) = \rho _0{\mathrm{exp}}[ - e{{\Phi }}(r)/(k_{\mathrm{B}}T)]\), which causes obvious underestimation of the electron density near the target ion, as shown in Fig. 5.

Fig. 5: Electron density fluctuations of ion embedded in ultra-cold neutral plasmas (UNP).
figure 5

a, b The electron density fluctuation \(\delta \rho \left( r \right)\) around an ion (Q = 1, at origin) embedded in the UNPs with a \(\rho _{\mathrm{e}} = 10^9\,{\mathrm{cm}}^{ - 3}\,{\mathrm{and}}\;T_{\mathrm{e}} = 5.5\,{\mathrm{K}}\) and b \(\rho _{\mathrm{e}} = 10^9\,{\mathrm{cm}}^{ - 3}\;{\mathrm{and}}\;T_{\mathrm{e}} = 11.5\,{\mathrm{K}}\). The distance r ranges from 0 to \(a_{{\mathrm{WS}}}/2 \approx 31,000\) Å. The classical molecular dynamic (CMD) simulated densities of electrons and free electrons are shown in square and triangle, respectively. Electron densities from Fermi–Dirac distribution (dash line), linear Debye–Hückel model (dash–dot–dot line), and the present model (solid line) are shown to check their reliabilities. And the free-electron density from the present model is shown in a short dash line.

Full size image

In order to further explore the effect of recombined bound electron distribution, the free-electron density distributions from the present model are compared to those from the CMD simulations. The good agreements are shown again in between the CMD and the present model. Note that free-electron density of the present model is the same as the one of Fermi–Dirac distribution. This indicates that the difference between the full Fermi–Dirac distribution and CMD simulation comes from the different treatments of the negative-energy electron distributions. According to our personal communication with Jie Yang and Feng Fang, the important contributions of the three-body recombination processes on the electron distribution of the target ion are observed lately in the UNPs experiment, in which a large amount of highly excited Rydberg state Rb atoms are found be produced from the three-body recombination processes between Rb+ ion and two free electrons of the surrounding plasma. It is tempted to conclude that Boltzmann or Fermi–Dirac distribution theory would be inapplicable to dense or moderately/strongly coupled plasmas where three-body recombination processes become important.

Note that only the static plasma screening effects are included in the present work. When modeling screaming plasmas or investigating the atomic processes with the non-negligible motion of ions in plasma43,44,45, the effects of dynamic screening should be further considered. For example, in the investigation of dynamic plasma screening effects on ion–ion collisions45, the static Debye–Hückel model is found to overestimate the plasma-screening effects on the electron capture process, and the dynamic screening effects can be reduced to the static plasmas screening effects when the velocity of projectile ion is smaller than the electron thermal velocity. The present model will be extended to consider the dynamic screening effect of dense plasmas in combination with the quantum statistical approach31 in our future work.

Conclusion

In summary, a universal electron screening model is proposed for treating the electron screening effects of dense or moderately/strongly coupled plasmas, in which the three-body recombination processes are found to be important in determining the electron density distribution around target ions in plasmas. Due to the quantum degeneracy effect between the recombined and initially bound electrons, the electron distribution of the target ion is sensitive to the specific bound state studied, which further influences the ion energy levels and line shifts. The proposed atomic-state-dependent model opens a promising way to treat the electron screening effect on atoms embedded in warm/hot dense plasma, which is essential for the investigation of atomic structure and dynamics in plasmas, as well as the spectra and EOS of plasma. Apart from the three-body recombination processes, this work constructs a theoretical framework to couple other inelastic collision and radiative processes to the screening effect, which will be considered in our future work. Next, we will further apply the present model to treat the plasmas with a wide range of temperatures and densities. We may devote machine learning technique46 to construct a more convenient analytic potential. This work is expected to provide an effective approach to handle those challenging questions existing in related studies of high-energy-density physics, such as astrophysical objects (stars, planets), inertial confinement fusion, and the matter properties in extreme conditions.

Methods

Numerical calculations

In the present screening model, total effective potential \({{\Phi }}({\boldsymbol{r}})\) and plasma-electron density fluctuation \(\delta \rho \left( {\boldsymbol{r}} \right)\) are numerically calculated by employing Eqs. (6) and (7). For a system with a given mean free-electron density \(\rho _{\mathrm{e}}\) and electron temperature Te, the chemical potential μ in Eq. (1) meets with

$$\rho _{\mathrm{e}} = \int _{p_0}^\infty \frac{1}{{1 + \exp \left[ {\frac{1}{{k_{\mathrm{B}}T_{\mathrm{e}}}}\left( {\frac{{p^2}}{{2m_{\mathrm{e}}}} - \mu } \right)} \right]}}p^2{\mathrm{d}}p,$$
(8)

and can be calculated by the accurate Padé approximants to the Fermi–Dirac integrals and their inversions47. Then \({{\Phi }}({\boldsymbol{r}})\) and \(\delta \rho \left( {\boldsymbol{r}} \right)\) are only dependent to each other and can be calculated with an iteration approach. Note that \({\mathbf{\Phi }}({\it{r}})\) and \(\delta \rho \left( {\it{r}} \right)\) decrease to zero exponentially at large r, which is similar with the one of Debye–Hückel model. The total effective potential energy \(V\left( {\boldsymbol{r}} \right)\) can be obtained as \(V\left( {\boldsymbol{r}} \right) = - e{{\Phi }}\left( {\boldsymbol{r}} \right)\) by using Eq. (7), in which the third term of \(\delta V\left( {\boldsymbol{r}} \right) = {\int} {\frac{{e^2}}{{4\pi \varepsilon _0\left| {{\boldsymbol{r}} - {\boldsymbol{r}}\prime } \right|}}\delta \rho ({\boldsymbol{r}}^\prime ){\mathrm{d}}{\boldsymbol{r}}^\prime }\) represents the perturbation one due to the presence of target ion.

Level-shift calculations

Once the plasma-electron density fluctuation is determined, the perturbation potential energy \(\delta V\left( {\boldsymbol{r}} \right)\) can be obtained. When the screening effects on an atom in state j are not very strong, the atomic energy level shift due to the presence of surrounding plasma can be calculated using the first-order perturbation theory

$$\delta \varepsilon _j = \int _0^\infty \left[ {P_j^2\left( r \right) + Q_j^2\left( r \right)} \right]\delta V\left( r \right)r^2{\mathrm{d}}r.$$
(9)

Here, \(P_j\left( r \right)\) and \(Q_j\left( r \right)\) are the relativistic radial wave functions of the large and small components, respectively. Compared with other models, the present model includes the contributions of three-body recombination processes and thus it is expected to be more accurate in the treatment of moderately/strongly coupled or dense plasmas.

In short, the atomic level shift in plasma can be computed with the present model with following steps: (I) the wave functions \(P_j\left( r \right)\) and \(Q_j\left( r \right)\) of the target ion are calculated using the multi-configuration Dirac–Fock approach; (II) the total effective potential \({{\Phi }}({\boldsymbol{r}})\) and the plasma-electron density fluctuation \(\delta \rho \left( {\boldsymbol{r}} \right)\) can be calculated using Eqs. (6) and (7) with an iteration method; (III) the atomic energy level shift can be obtained with Eq. (9) based on the first-order perturbation theory.