Introduction

Cavity optomechanical systems are the leading platform for the detection and manipulation of mechanical oscillators with electromagnetic fields from the nano- to the macroscale1. Displacement detection with an imprecision below the standard quantum limit2,3, sideband cooling to the motional quantum groundstate4,5, the preparation of nonclassical states of motion6,7,8,9, quantum entanglement of distinct mechanical oscillators10,11, topological energy transfer using exceptional points12, and microwave-to-optical-frequency transducers13,14 are just some of the highlights that have been reported during the last decade. All of these impressive results have been achieved with linear cavities, linear mechanical oscillators, and in the linearized regime of the optomechanical interaction utilizing large-amplitude cavity control fields, which however limits the available possibilities for mechanical-state detection and control.

Very recently, an exciting scheme to couple a mechanical oscillator to microwave photons in a superconducting LC circuit has been realized: flux-mediated optomechanical coupling15,16,17,18. In this approach, the displacement of a mechanical oscillator is transduced to magnetic flux threading a superconducting quantum-interference device (SQUID) embedded in a microwave LC circuit as flux-dependent inductance19,20,21. Due to the scaling of the optomechanical single-photon coupling rate g0 with the external magnetic transduction field in flux-mediated optomechanics15,21, record single-photon coupling rates for the microwave domain have been reported16,17,18 and achieving the long-sought-after optomechanical single-photon regime22,23 or even the ultrastrong coupling to superconducting qubits24 seems feasible in future devices.

Naturally, this platform comes along with its own opportunities and challenges. First, a SQUID constitutes a nonnegligible Kerr nonlinearity, which is typically undesired in optomechanics, as it, for instance, limits the maximally applicable power of a red-sideband cooling tone due to the appearance of an exceptional point and a bifurcation instability in the Kerr cavity susceptibility25. Nevertheless, intrinsic nonlinearities and parametrically driven cavities are also potentially promising resources for optomechanical systems and have attracted increasing interest in this context lately20,26,27,28,29,30,31. Second, SQUIDs are extremely flux-sensitive devices and therefore flux-mediated optomechanics is susceptible to flux noise, which can lead to fluctuating-cavity frequencies, an effect unwanted in optomechanical protocols. When dealing with nonlinear systems, frequency fluctuations are particularly challenging as they can cause the cavity to switch unexpectedly across the bifurcation threshold at high driving powers. Developing protocols to work around these challenges is of utmost importance for any optomechanical system composed of noisy cavities and Kerr nonlinearities, and flux-mediated optomechanics is the ideal platform to study these regimes in a highly designable and flexible scenario.

Here, we engineer a flux-mediated optomechanical device with a large single-photon coupling rate of up to g0 ≈ 2π ⋅ 3.6 kHz and demonstrate sideband cooling of the mechanical oscillator close to its quantum groundstate by intracavity four-wave mixing (4WM). The four-wave cooling scheme we implement here demonstrates how the cavity Kerr nonlinearity itself can be utilized for reducing cavity-frequency noise and for evading the Kerr cavity bifurcation instability in optomechanical sideband cooling. By using a strong parametric cavity drive, we activate the emergence of two Kerr quasi-modes in the SQUID circuit and realize an optomechanical coupling of these quasi-modes to the mechanical oscillator by an additional optomechanical sideband-pump field. The drive-activated Kerr modes show enhanced properties such as a reduced effective linewidth compared with the undriven circuit, and in particular, a suppression of cavity-frequency fluctuations by an internal stabilization-feedback loop. In this scheme, we achieve effective single-photon cooperativities \({{{{{{{{\mathcal{C}}}}}}}}}_{{{{{{{{\rm{0}}}}}}}}}\,\gtrsim\, 10\) and strikingly find that blue-detuned optomechanical sideband pumping leads to dynamical backaction with the characteristics of red-sideband pumping in a standard optomechanical system, in particular to positive optical damping. This surprising result is a consequence of sideband interference due to 4WM and allows to evade the Kerr bistability that is only relevant for red-detuned pumping. We finally use this blue-detuned optical damping to cool the mechanical oscillator to a residual occupation of nm ~ 1.6. Our results demonstrate how cavity Kerr nonlinearities can be used in optomechanics to achieve both, enhanced device performance and unexplored control schemes for mechanical oscillators. At the same time, they reveal the potential of flux-mediated optomechanics regarding low-power groundstate cooling of mechanical oscillators and the future preparation of quantum states of motion.

Results

The device

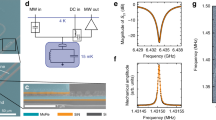
Our device combines a superconducting quantum-interference LC circuit with a mechanical nanobeam oscillator embedded into the loop of the SQUID, cf. Fig. 1a–c. Details on device fabrication are given in Supplementary Note 1. At the core of the circuit, the SQUID acts as a magnetic-flux-dependent inductance LS(Φ), where Φ is the total magnetic flux threading the 21 × 3 μm2 large loop. For the tunable optomechanical coupling between the displacement of the mechanical nanobeam and the microwave circuit, two distinct external magnetic fields are required. First, a magnetic field perpendicular to the chip surface B⊥ is used to change the magnetic-flux bias Φ⊥ through the SQUID loop, allowing to tune the circuit resonance frequency ω0 and flux responsivity \({{{{{{{\mathcal{F}}}}}}}}=\partial {\omega }_{0}/\partial \varPhi\). Second, a magnetic in-plane field B∥ is used to transduce the out-of-plane displacement δx of the mechanical oscillator to additional flux Φ∥ = B∥lmδx, where lm = 18 μm is the length of the mechanical beam. To apply these two fields, the chip is mounted into a homemade 2D vector magnet, consisting of a large split coil for B∥ and an additional small coil mounted below the chip for the generation of B⊥, cf. Fig. 1d. The whole configuration is placed in a cryoperm magnetic shielding and attached to the mK plate of a dilution refrigerator with a base temperature Tb ≈ 15 mK. More details on the measurement setup are given in Supplementary Notes 2 and 3.

Fig. 1: A superconducting quantum-interference cavity parametrically coupled to a mechanical nanobeam.
figure 1

a Optical micrograph of the circuit. Bright parts are aluminum, dark parts are silicon substrate. The LC circuit combines two interdigitated capacitors (IDCs) C with two linear inductors L, connected through a superconducting quantum-interference device (SQUID) with total Josephson inductance LS = LJ/2. The circuit is capacitively coupled to a Z0 = 50 Ω coplanar waveguide feedline (top of image) with a coupling capacitor Cc and surrounded by ground plane. b Scanning electron micrograph of the constriction-type SQUID, showing the two Josephson junctions and the mechanical oscillator as part of the loop released from the substrate. The inset shows a zoom-in to one of the nanobridge Josephson junctions. c Circuit equivalent of the device. For the experiments, two magnetic fields can be applied. The field B⊥ is oriented perpendicular to the chip plane and is used to set the flux-bias working point of the SQUID Φ⊥. The parallel field B∥ transduces mechanical displacement of the out-of-plane mode to additional flux Φ∥ = B∥lδx threading the SQUID loop. d shows the sample integrated into a printed-circuit board with two microwave connectors and mounted into a 2D vector magnet. The large split coil is used to generate B∥, a small single coil behind the chip generates B⊥. e Transmission response ∣S21∣ of the cavity at B∥ = 25 mT and B⊥ = 0. From a fit to the data, we extract the resonance frequency ω0 = 2π ⋅ 5.2673 GHz, the total linewidth κ = 2π ⋅ 380 kHz, and the external linewidth κe = 2π ⋅ 110 kHz. Data are shown as circles, fit as black line. f Resonance frequency ω0 vs magnetic flux Φ⊥, normalized to one-flux quantum Φ0 at B∥ = 25 mT. Circles are data, line is a fit. The two operation points for this paper are marked with stars and denoted “I” for ω0 ≈ 2π ⋅ 5.22 GHz and “II” for ω0 ≈ 2π ⋅ 5.17 GHz. Details on measurements and fits can be found in Supplementary Note 4.

Full size image

We perform the experiments presented here at in-plane fields of B∥ = 21 mT and B∥ = 25 mT. Figure 1e shows the transmission response of the cavity for B∥ = 25 mT and at the bias-flux sweetspot. It has a resonance frequency ω0 = 2π ⋅ 5.2673 GHz, a total linewidth κ = 2π ⋅ 380 kHz, and an external linewidth κe = 2π ⋅ 110 kHz. Figure 1f shows how the cavity resonance frequency can be tuned by ~150 MHz by changing the applied flux bias Φ⊥ threading the SQUID loop. The curves and cavity parameters at B∥ = 21 mT only deviate slightly from the ones given here, the corresponding additional data can be found in Supplementary Note 4. Due to an improved SQUID design and fabrication, the cavity-flux responsivity \({{{{{{{\mathcal{F}}}}}}}}\) is increased by one order of magnitude compared with our previous results15, which leads to a significantly enhanced single-photon coupling rate

$${g}_{0}={{{{{{{\mathcal{F}}}}}}}}{B}_{\parallel }{l}_{{{{{{{{\rm{m}}}}}}}}}{x}_{{{{{{{{\rm{zpf}}}}}}}}}$$
(1)

where xzpf is the mechanical zero-point fluctuation amplitude.

The mechanical nanobeam, visible in Fig. 1b and released from the substrate in an isotropic reactive ion-etching process using SF6 plasma32, is 500 nm wide and 70 nm thick. From its total mass of m ≈ 1.9 pg and the resonance frequency of the out-of-plane mode Ωm ≈ 2π ⋅ 5.32 MHz, we get \({x}_{{{{{{{{\rm{zpf}}}}}}}}}=\sqrt{\frac{\hslash }{2m{\varOmega }_{{{{{{{{\rm{m}}}}}}}}}}}\approx 30\,\)fm. For an in-plane field of B∥ = 25 mT, and the two flux-bias points ΦI and ΦII, cf. Fig. 1f, we obtain single-photon coupling rates g0,I = 2π ⋅ 1.9 kHz and g0,II = 2π ⋅ 3.6 kHz with \({{{{{{{{\mathcal{F}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}=2\pi \cdot 300\,\)MHz/Φ0 and \({{{{{{{{\mathcal{F}}}}}}}}}_{{{{{{{{\rm{II}}}}}}}}}=2\pi \cdot \,520\,\)MHz/Φ0. For the smaller in-plane field of B∥ = 21 mT, the g0-values are scaled accordingly, cf. Supplementary Note 5.

The final important parameter of the device is its Kerr nonlinearity, which at the flux sweetspot is \({{{{{{{\mathcal{K}}}}}}}}/2\pi =-30\,\)kHz. For the two flux-bias operation points I and II, we obtain \({{{{{{{{\mathcal{K}}}}}}}}}_{{{{{{{{\rm{I}}}}}}}}}/2\pi =-40\,\)kHz and \({{{{{{{{\mathcal{K}}}}}}}}}_{{{{{{{{\rm{II}}}}}}}}}/2\pi =-55\,\)kHz, respectively. More details on the determination of the circuit parameters and their flux dependence can be found in Supplementary Note 4.

Driven Kerr modes and dynamical Kerr backaction

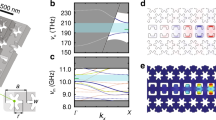
Owing to the Kerr anharmonicity \({{{{{{{\mathcal{K}}}}}}}}\), the application of a strong microwave-drive tone close to the cavity resonance frequency ω0 significantly modifies the cavity response to an additional probe field. In Fig. 2, we discuss this modified response in the presence of a parametric drive tone with a fixed frequency ωd, when the cavity is tuned to cross this drive tone by means of the bias field B⊥. For large detunings between cavity and drive, the circuit response S21 exhibits a standard single-mode resonance lineshape. However, as the detuning Δd = ωd − ω0 is reduced, the driven-cavity susceptibility

$${\chi }_{{{{{{{{\rm{g}}}}}}}}}(\varOmega )=\frac{{\tilde{\chi }}_{{{{{{{{\rm{p}}}}}}}}}(\varOmega )}{1-{{{{{{{{\mathcal{K}}}}}}}}}^{2}{n}_{{{{{{{{\rm{d}}}}}}}}}^{2}{\tilde{\chi }}_{{{{{{{{\rm{p}}}}}}}}}(\varOmega ){\tilde{\chi }}_{{{{{{{{\rm{p}}}}}}}}}^{* }(-\varOmega )}$$
(2)

deviates considerably from a single linear cavity, leading to the regime of parametric amplification and degenerate four-wave mixing, which is experimentally identified by the appearance of a second mode, cf. Fig. 2a, b. Here, Ω = ω − ωd denotes the detuning between the probe field at ω and the parametric drive and

$${\tilde{\chi }}_{{{{{{{{\rm{p}}}}}}}}}(\varOmega )=\frac{1}{\frac{\kappa }{2}+{{{{{{{\rm{i}}}}}}}}\left({\varDelta }_{{{{{{{{\rm{d}}}}}}}}}-2{{{{{{{\mathcal{K}}}}}}}}{n}_{{{{{{{{\rm{d}}}}}}}}}+\varOmega \right)}.$$
(3)
Fig. 2: Cavity stabilization by activation of the Kerr quasi-mode state and single-tone dynamical Kerr backaction.
figure 2

a Color-coded magnitude of the SQUID cavity response S21 vs SQUID flux bias Φ⊥/Φ0 in the presence of a strong drive at ωd. The flux-bias range corresponds to a small variation of Φ⊥ around operation point I and B∥ = 25 mT. When the flux-tunable resonance frequency ω0, indicated as dashed line and labeled “Drive off”, is far detuned from the drive tone, the cavity response exhibits a single broad absorption resonance. As the detuning between cavity and drive Δd = ωd − ω0 is reduced, the cavity response is significantly modified and the original resonance is developing into a double-mode structure. The appearance of these driven Kerr quasi-modes indicates the onset of parametric amplification and degenerate 4WM in the SQUID circuit. We denote the two modes as signal and idler resonance with the resonance frequencies ωs and ωi, respectively. The arrow on the left indicates the position of the linescan shown in panel b. In addition to the linescan from a (red circles) and the result of the analytical response calculation (solid black line), we show the equivalent linescan without parametric drive (blue circles) and its corresponding theoretical response (dashed black line). The curves without parametric drive are offset by + 5 dB for clarity. Panels c and d show ωs and effective linewidth \(\kappa ^{\prime}\) of the signal resonance vs flux bias. Lines show the result of modeling the effective quantities with the driven Kerr cavity equations and taking into account flux-noise broadening and two-level systems. The stabilized regime of operation is indicated by dashed lines and shaded areas. Here, the linewidth is nearly constant with \(\kappa ^{\prime} /2\pi \approx 340\,\)kHz. The width of the operation range corresponds to the flux-noise standard deviation, which we estimate to be σΦ ~ 5 mΦ0. Panel e illustrates the dynamical Kerr backaction of the drive fields to the nanobeam. Optomechanical (OM) up- and downscattering induces cooling and heating/amplification to the mechanical mode, respectively, where gα is the multiphoton coupling rate and χg is the probe-field susceptibility. In addition, interference between up- and downscattered fields due to degenerate 4WM has to be taken into account. f and g show the calculated optical spring and optical damping. The two blue/red lines and shaded area correspond to g0/2π = (1.95 ± 0.1) kHz. The detuning range Δd is slightly increased compared with a–d. In the additional range, the backaction is plotted in gray.

Full size image

The two Kerr quasi-modes, which we denote as signal and idler resonance, appear symmetrically around the drive with complex resonance frequencies

$${\omega }_{i/s}={\omega }_{{{{{{{{\rm{d}}}}}}}}}+{{{{{{{\rm{i}}}}}}}}\frac{\kappa }{2}\pm \sqrt{\left({\varDelta }_{{{{{{{{\rm{d}}}}}}}}}-{{{{{{{\mathcal{K}}}}}}}}{n}_{{{{{{{{\rm{d}}}}}}}}}\right)\left({\varDelta }_{{{{{{{{\rm{d}}}}}}}}}-3{{{{{{{\mathcal{K}}}}}}}}{n}_{{{{{{{{\rm{d}}}}}}}}}\right)}$$
(4)

where nd is the parametric drive intracavity photon number. These Kerr modes have been observed and discussed also in the context of optical cavities and mechanical oscillators33,34,35. The signal mode can be identified by the shifted and significantly deepened cavity absorption dip and the idler mode by the resonance peak, indicating net transmission gain by Josephson parametric amplification.

With the activation of the quasi-mode state, we obtain a highly stabilized effective resonance frequency and linewidth, while the bare cavity suffers from considerable frequency fluctuations due to flux noise. Due to the reduction of frequency fluctuations in combination with a saturation of two-level system losses by the parametric drive (cf. Supplementary Note 6), the effective cavity linewidth is reduced from the flux-noise broadened \({\kappa }_{{{{{{{{\rm{off}}}}}}}}}^{\prime} \sim 2\pi \cdot 1.5\,\)MHz to the driven \({\kappa }_{{{{{{{{\rm{on}}}}}}}}}^{\prime}\approx 2\pi \cdot 340\,\)kHz. An analysis of the signal-mode resonance frequency and linewidth in the presence of the parametric drive is provided in Fig. 2c, d. Within a small region of flux-bias values, the drive-tone-induced Kerr shift compensates for the flux-noise-induced frequency shifts by means of an internal feedback loop. The working principle of this internal feedback is simple: when the bare cavity frequency shifts due to a change in SQUID flux, the intracavity drive–photon number nd gets adjusted by this new detuning Δd between bare cavity and drive. As a consequence, the quasi-mode frequencies, which depend on both Δd and the Kerr term \({{{{{{{\mathcal{K}}}}}}}}{n}_{{{{{{{{\rm{d}}}}}}}}}\), cf. Eq. (4), remain nearly constant. Strikingly, this mechanism yields an internal stabilization of the driven resonance and minimizes the impact of flux noise, which thereby becomes the natural choice of operation regime during the following experiments.

In an optomechanical system, any intracavity field also acts back on the mechanical oscillator by altering its resonance frequency and decay rate, an effect known as dynamical backaction36,37. Therefore, the effect of the parametric drive to the mechanical oscillator also requires some careful consideration. To model this, we use the linearized equations of motion for the mechanical amplitude field \(\hat{b}\) and the intracavity fluctuation field \(\hat{a}\) in a single-tone-driven Kerr cavity

$$\dot{\hat{b}}=\left({{{{{{{\rm{i}}}}}}}}{\varOmega }_{{{{{{{{\rm{m}}}}}}}}}-\frac{{\varGamma }_{{{{{{{{\rm{m}}}}}}}}}}{2}\right)\hat{b}-{{{{{{{\rm{i}}}}}}}}{g}_{\alpha }\left(\hat{a}+{\hat{a}}^{{{{\dagger}}} }\right)+\sqrt{{\varGamma }_{{{{{{{{\rm{m}}}}}}}}}}\hat{\zeta }$$
(5)
$$\dot{\hat{a}}= \left[-{{{{{{{\rm{i}}}}}}}}({\varDelta }_{{{{{{{{\rm{d}}}}}}}}}-2{{{{{{{\mathcal{K}}}}}}}}{n}_{{{{{{{{\rm{d}}}}}}}}})-\frac{\kappa }{2}\right]\hat{a}+{{{{{{{\rm{i}}}}}}}}{{{{{{{\mathcal{K}}}}}}}}{n}_{{{{{{{{\rm{d}}}}}}}}}{\hat{a}}^{{{{\dagger}}} }\\ -{{{{{{{\rm{i}}}}}}}}{g}_{\alpha }\left(\hat{b}+{\hat{b}}^{{{{\dagger}}} }\right)+\sqrt{{\kappa }_{{{{{{{{\rm{i}}}}}}}}}}{\hat{\xi }}_{{{{{{{{\rm{i}}}}}}}}}+\sqrt{{\kappa }_{{{{{{{{\rm{e}}}}}}}}}}{\hat{\xi }}_{{{{{{{{\rm{e}}}}}}}}}$$
(6)

with multiphoton coupling rate \({g}_{\alpha }=\sqrt{{n}_{{{{{{{{\rm{d}}}}}}}}}}{g}_{0}\) and input-noise fields \(\hat{\zeta }\), \({\hat{\xi }}_{{{{{{{{\rm{i}}}}}}}}}\) and \({\hat{\xi }}_{{{{{{{{\rm{e}}}}}}}}}\)1,4. The input-noise fields describe drive fields related to the thermal and quantum baths of the oscillators, more details can be found in Supplementary Note 7. From the equations of motion, the effective mechanical susceptibility can be derived as

$${\chi }_{0}^{{{{{{{{\rm{eff}}}}}}}}}(\varOmega )=\frac{1}{\frac{{\varGamma }_{{{{{{{{\rm{m}}}}}}}}}}{2}+{{{{{{{\rm{i}}}}}}}}\left(\varOmega -{\varOmega }_{{{{{{{{\rm{m}}}}}}}}}\right)+{\Sigma }_{{{{{{{{\rm{k}}}}}}}}}({\varOmega }_{{{{{{{{\rm{m}}}}}}}}})}$$
(7)

for the weak-coupling and high-Qm limit, which is safely fulfilled for our mechanical oscillator with a linewidth of Γm ≈ 2π ⋅ 13 Hz. The single-tone dynamical Kerr backaction

$${\Sigma }_{{{{{{{{\rm{k}}}}}}}}}({\varOmega }_{{{{{{{{\rm{m}}}}}}}}})={g}_{\alpha }^{2}\left[{\chi }_{{{{{{{{\rm{g}}}}}}}}}\left(1-\overline{{{{{{{{\mathcal{A}}}}}}}}}\right)-{\overline{\chi }}_{{{{{{{{\rm{g}}}}}}}}}\left(1-{{{{{{{\mathcal{A}}}}}}}}\right)\right]$$
(8)

with χg = χg(Ωm) and \({\overline{\chi }}_{{{{{{{{\rm{g}}}}}}}}}={\chi }_{{{{{{{{\rm{g}}}}}}}}}^{* }(-{\varOmega }_{{{{{{{{\rm{m}}}}}}}}})\) has almost the same form as in linear optomechanics, but with a modified cavity susceptibility χg. A striking difference, however, is found in the terms \({{{{{{{\mathcal{A}}}}}}}}=-{{{{{{{\rm{i}}}}}}}}{{{{{{{\mathcal{K}}}}}}}}{n}_{{{{{{{{\rm{d}}}}}}}}}{\tilde{\chi }}_{{{{{{{{\rm{p}}}}}}}}}({\varOmega }_{{{{{{{{\rm{m}}}}}}}}})\) and \(\overline{{{{{{{{\mathcal{A}}}}}}}}}={{{{{{{\rm{i}}}}}}}}{{{{{{{\mathcal{K}}}}}}}}{n}_{{{{{{{{\rm{d}}}}}}}}}{\tilde{\chi }}_{{{{{{{{\rm{p}}}}}}}}}^{* }(-{\varOmega }_{{{{{{{{\rm{m}}}}}}}}})\). These terms correspond to an interference of the red and blue mechanical sideband fields, which occurs due to intracavity four-wave mixing in a driven Kerr cavity. By this 4WM, the two standard mechanical sidebands become idler fields of each other. A schematic of the dynamical backaction and the sideband interference is shown in Fig. 2e.

The optical spring \(\delta {\varOmega }_{{{{{{{{\rm{m}}}}}}}}}=-{{{{{{{\rm{Im}}}}}}}}\left[{\Sigma }_{{{{{{{{\rm{k}}}}}}}}}({\varOmega }_{{{{{{{{\rm{m}}}}}}}}})\right]\) and optical damping \({\varGamma }_{{{{{{{{\rm{opt}}}}}}}}}=2{{{{{{{\rm{Re}}}}}}}}\left[{\Sigma }_{{{{{{{{\rm{k}}}}}}}}}({\varOmega }_{{{{{{{{\rm{m}}}}}}}}})\right]\) caused by the dynamical Kerr backaction are displayed in Fig. 2f, g. When the drive is located around one mechanical frequency detuned from the cavity ∣Δd∣ ≈ Ωm = 2π ⋅ 5.32 MHz, the backaction looks very similar to that of a linear cavity. However, when the drive and the cavity are near-resonant, the backaction is strongly dominated by the intracavity photon number and a Duffing-like behavior can be observed with a sudden transition from high- to low-amplitude state at Δd ≈ − 2π ⋅ 3 MHz. In the operation regime for the experiments described here, the drive-induced backaction for operation point I is small with Γopt/2π ~ − 1 Hz and δΩm/2π ~ − 5 Hz. Using the bare mechanical linewidth Γm ~ 2π ⋅ 13 Hz, the corresponding phonon occupation is therefore increased by about 10%, a detailed calculation and discussion of the resulting mechanical-mode occupation is given in Supplementary Note 7.

Due to the considerable cavity flux noise outside of the driven quasi-mode regime, we unfortunately cannot experimentally access the dynamical Kerr backaction for the detuning range shown in Fig. 2. Nevertheless, with a larger single-photon coupling rate g0 at operation point II and a stronger drive tone, we observe regimes of mechanical instability induced by the dynamical Kerr backaction, which are in excellent agreement with the prediction from the theory. The corresponding data and analysis are explained in detail in Supplementary Note 7. The presented formalism for the dynamical Kerr backaction can also directly be applied to the sideband-unresolved regime and explains the experimental findings of a recent experiment with a similar SQUID cavity optomechanical device16, cf. also Supplementary Note 7.

Multitone dynamical four-wave backaction

An interesting question arising now is how the Kerr quasi-modes couple to the mechanical nanobeam, when an additional optomechanical pump tone is applied to one of the Kerr-mode sidebands. One might expect that the coupling to the mechanical oscillator is suppressed in this state, similar to the reduced impact of flux noise, as the Kerr-mode frequencies ωs and ωi display only a very weak dependence on flux through the SQUID. Fluctuations of the bare resonance frequency, however, lead to modulations of αd and parametric gain, and therefore will impact the mechanical oscillator by inducing changes in the radiation-pressure force. A straightforward way to investigate this setting experimentally is to apply an additional optomechanical pump tone on the red sideband of the signal resonance, i.e., with a pump frequency ωp ≈ ωs − Ωm. Once in this configuration, a weak probe signal around ω ≈ ωp + Ωm can be used to detect optomechanically induced transparency (OMIT)38 and thereby characterize the optomechanical interaction. A detailed theoretical description as well as a discussion of the experimental findings for this red-sideband pumping setup is given in Supplementary Notes 12–15.

A conceptually less straightforward and more exciting possibility is to pump the idler resonance on its blue sideband ωp ≈ ωi + Ωm, cf. Fig. 3a. A blue-detuned pump is commonly associated with amplification/heating due to the favored Stokes scattering to lower-energy photons. The Kerr-mode susceptibility χg close to the idler resonance, however, resembles that of an “inverted” mode. Any small intracavity field in the driven Kerr cavity experiences in addition a mirroring effect due to degenerate four-wave mixing with the parametric drive tone. The presence of the blue-sideband pump field enriches this situation even further. Then, the Kerr cavity is effectively oscillating with Ωdp = ωd − ωp due to the presence of two strong fields, and the effects arising from nondegenerate four-wave mixing (cross-mixing) can impact probe fields and mechanical sideband fields and finally also the OMIT response and the backaction to the mechanical oscillator.

Fig. 3: Four-wave OMIT and four-wave backaction for optomechanical blue-sideband pumping of the idler quasi-mode.
figure 3

a Experimental protocol. The SQUID cavity is prepared in the quasi-mode state by a strong parametric drive (PD). In addition, an optomechanical (OM) pump tone is applied on the blue sideband of the idler resonance (IR) ωp = ωi + Ωm + δp. Finally, we use a weak probe tone around the signal resonance (SR) to detect optomechanically induced transparency. We repeat this scheme for varying detunings δp. b explains how this protocol to the first order leads to coherent driving of the mechanical oscillator. By PD-induced intracavity 4WM, the OM pump (probe tone) gets an idler field on the opposite side of the drive, which has the right detuning to the probe tone (pump) ~ Ωm to coherently drive the mechanical oscillator. c shows the signal resonance transmission S21 measured with the weak probe field (OM pump off). Circles are data, line is a fit. Vertical bars labeled with A, B, and C indicate zoom regions for the corresponding panels shown in c and Δs = ω − ωs denotes the detuning between probe field and SR. d Probe tone response (OM pump on) in three narrow-frequency windows around ω ≈ 2ωd − ωp + Ωm for three different pump detunings δp, cf. panel a. Note that the frequency difference between OM pump and probe field is Ω ≈ Ωm − 2Ωdp, which implies that when the pump-field frequency is reduced, the probe-field frequency is increasing. Each probe-tone response displays a narrow-band resonance, indicating optomechanically induced transparency (OMIT) via excitation of the mechanical oscillator. For each δp, we fit the OMIT response (lines in c) and extract the effective mechanical resonance frequency Ωeff = Ωm + δΩm and the effective mechanical linewidth Γeff = Γm + Γopt. The contributions δΩm and Γopt, induced by dynamical backaction of all intracavity fields, are plotted in panels e and f as circles vs δp. The result of analytical calculations is shown as two solid lines with shaded area, where the range described by the lines captures uncertainties in the device parameters, cf. Supplementary Note 11. The dashed line shows the result of equivalent calculations without cross-mixing (nondegenerate 4WM) terms. g illustrates schematically one four-wave cross-mixing term that leads to the observed dynamical backaction. Hereby, two mechanical sidebands with frequency difference Ωdp = ωd − ωp and both, the PD and the OM pump, contribute to the interaction. For the data in c–f, B∥ = 21 mT, g0 = 2π ⋅ 1.75 kHz, and nd ≈ 69 ± 11.

Full size image

A clear signature of the parametric state and four-wave mixing is the appearance of optomechanically induced transparency in the probe response of the signal resonance, when the idler Kerr mode is pumped on its blue sideband. Corresponding data are shown in Fig. 3c, d. Here and in stark contrast to the usual OMIT protocol, the frequency detuning between the idler blue-sideband pump and the probe tone is not even close to the mechanical resonance frequency but given by Ω = ω − ωp ≈ 2Ωdp + Ωm. To first order, the observation of this transparency can be understood by considering the intracavity-generated tones in addition to the ones that are sent externally. The parametric drive generates an intracavity field with amplitude αd at ωd, and the optomechanical pump at ωp generates an intracavity field with amplitude γ−. Just by this doubly driven configuration, a third intracavity “pump” field is generated by degenerate 4WM at ω+ = ωp + 2Ωdp and we denote its amplitude as γ+. Therefore, when ωp = ωi + Ωm, the γ+-field is located at the red sideband of the signal resonance ω+ = ωs − Ωm. The beating between a probe field at ω ≈ ωs and the γ+-field is then near-resonant with the mechanical oscillator and will drive it into coherent motion. A second beating component, which is driving the mechanical oscillator, originates from the beating of the γ−-field and the idler field of the weak probe itself, cf. Fig. 3b. These two are also near-resonant with the mechanical oscillator. Once in coherent motion, the mechanical oscillator generates sidebands to all intracavity-field Fourier components, some of which interfere with the original probe tone, causing the observed appearance of four-wave OMIT.

To characterize the dynamical backaction imprinted by the intracavity fields on the mechanical oscillator in the presence of the αd, γ−, and γ+ fields, we measure the optomechanical transparency response for varying detuning δp between the γ−-field and the idler-mode blue sideband. For each detuning, we determine the effective mechanical resonance frequency Ωeff and effective mechanical linewidth Γeff from a fit to the transparency signal and subtract the intrinsic values Ωm and Γm. The remaining contributions to the resonance frequency and linewidth δΩm and Γopt, respectively, correspond to the optical spring and optical damping by the microwave fields.

The result, shown in Fig. 3e, f, is quite surprising. Even though the optomechanical pump field is blue-detuned to all cavity resonances ω0, ωs, and ωi, we observe dynamical backaction with characteristics resembling red-sideband pumping in linear optomechanical systems. Most strikingly, we find a positive optical damping, which is usually a clear signature for red-sideband physics and the basis for sideband cooling of the mechanical mode4. We use a linearized, optomechanical multitone Kerr cavity model, and implement the hierarchy from the experiment \({\alpha }_{{{{{{{{\rm{d}}}}}}}}}\gg {\gamma }_{\mp }\gg \langle \hat{a}\rangle\) to reveal which interactions are responsible for the observed behavior, cf. Supplementary Notes 8–10. The resulting effective mechanical susceptibility

$${\chi }_{0}^{{{{{{{{\rm{eff}}}}}}}}}(\varOmega )=\frac{1}{\frac{{\varGamma }_{{{{{{{{\rm{m}}}}}}}}}}{2}+{{{{{{{\rm{i}}}}}}}}\left(\varOmega -{\varOmega }_{{{{{{{{\rm{m}}}}}}}}}\right)+{\Sigma }_{{{{{{{{\rm{fw}}}}}}}}}({\varOmega }_{{{{{{{{\rm{m}}}}}}}}})}$$
(9)

has still the same form as for a standard optomechanical system, and all the 4WM contributions can be captured in \({{{{{{{\mathcal{J}}}}}}}}\)-factors in the dynamical four-wave backaction

$${{{\Sigma }}}_{{{{{{{{\rm{fw}}}}}}}}}({\varOmega }_{m})=\mathop{\sum }\limits_{j=-,\alpha ,+}^{}| {g}_{j}{| }^{2}\left[{\chi }_{{{{{{{{\rm{g}}}}}}}},j}{{{{{{{{\mathcal{J}}}}}}}}}_{j}-{\overline{\chi }}_{{{{{{{{\rm{g}}}}}}}},j}{\overline{{{{{{{{\mathcal{J}}}}}}}}}}_{j}\right]$$
(10)

with g− = γ−g0, g+ = γ+g0, χg,- = χg(Ωm), χg,α = χg(Ωm + Ωdp) and χg,+ = χg(Ωm + 2Ωdp). Closed-form expressions for the \({{{{{{{\mathcal{J}}}}}}}}\) are given in Supplementary Note 9. We identify nondegenerate four-wave mixing terms in the \({{{{{{{\mathcal{J}}}}}}}}\)-factors as the dominant origin of the observed backaction. These terms have contributions from the drive field αd, from one of the γ± fields, and couple any two distinct mechanical sidebands that have the frequency difference ±Ωdp, cf. Fig. 3g for a schematic of one of these terms. Hence, these terms correspond to intracavity cross-mixing based on αd and γ± fields. Using independently determined system parameters, we find excellent agreement between the experimental data and the analytical model when we take these cross-mixing terms into account, cf. solid lines in Fig. 3e, f. If we take only the degenerate 4WM terms into account, which are induced by the presence of αd, we find a small and nearly constant backaction for all δp, cf. dashed lines.

Blue-detuned four-wave cooling close to the groundstate

Positive optical damping is commonly related to cooling of the mechanical mode. Therefore, the blue-detuned pumping scheme described in Fig. 3 seems feasible to be utilized as a counterintuitive, yet innovative, method to eliminate the residual thermal excitations in the mechanical resonator. It is a particularly exciting option here, as blue-detuned pumping offers the opportunity to evade the Kerr bistability of the cavity, which becomes more relevant with increasing sideband-pump power.

To characterize the mechanical mode temperature, we detect the upconverted thermal displacement fluctuations in the signal resonance output field with a spectrum analyzer. For this measurement, the SQUID cavity in the quasi-mode state is pumped with an optomechanical tone on the blue sideband of the idler mode. Using a probe tone, we then measure the signal-mode response S21 in a wide-frequency range and the OMIT response in a narrow range. Finally, we detect the output spectrum in the same frequency window where the OMIT is observed, cf. also Fig. 4a. A collection of spectra for varying optomechanical pump power Pp is presented in Fig. 4b. From a careful analysis of the combined datasets, cf. Supplementary Notes 8–13, the equilibrium phonon occupation of the mechanical oscillator as well as the phonon occupation resulting from four-wave cooling can be inferred.

Fig. 4: Blue-detuned four-wave-cooling of a mechanical oscillator close to its quantum groundstate.
figure 4

a Schematic representation of the experiment. A parametric drive is used to activate the quasi-mode state and an optomechanical (OM) pump is sent to the blue sideband of the idler resonance ωp ≈ ωi + Ωm. The signal resonance output power spectral density is measured using a spectrum analyzer around ω = ωp + 2Ωdp + Ωm ≈ ωs. b Power spectral densities normalized to the optomechanical pump input power Pp for various pump powers. Frequency axis is given with respect to ω = ωp + 2Ωdp + Ωm. With increasing pump power, the linewidth of the upconverted mechanical noise spectrum is increasing, indicating four-wave dynamical backaction damping. Simultaneously, the area of the normalized signal decreases, indicating cooling of the mode. From fits (lines and shaded areas) to the data (points), we determine the resulting phonon occupation nm. In c, we show the cooled phonon number vs Γeff/Γm in a collection of sever`al different datasets. Intracavity drive photon numbers vary between different points in the range 30 < nd < 110. Circles correspond to data from measurements at operation point I and squares to data from operation point II. Stars show the points that correspond to the data shown in b, taken at operation point I. All measurements have been taken at B∥ = 25 mT. The inset shows the result of a thermal calibration measurement, indicating that the mechanical oscillator mode equilibrates with the fridge base temperature and the residual thermal occupation at Tb = 15 mK is \({n}_{{{{{{{{\rm{m}}}}}}}}}^{{{{{{{{\rm{th}}}}}}}}}\approx 70-90\). Dashed lines and shaded area display the theoretically calculated range of four-wave-cooled phonon occupation, taking into account a possible range of \(60\le {n}_{{{{{{{{\rm{m}}}}}}}}}^{{{{{{{{\rm{th}}}}}}}}}\le 100\) and 45 ≤ nd ≤ 90. Parametric amplification of cavity quantum noise limits the minimally achievable phonon occupation in our parameter regime to \({n}_{{{{{{{{\rm{m}}}}}}}}}^{\lim } \sim 0.6\). For the highest powers, we exceed this theoretical limit by only a factor ~3. d shows the effective effective mechanical linewidth vs intracavity sideband photon number nγ = ∣γ−∣2 + ∣γ+∣2 for points from c, which have nearly constant nd ≈ 87 ± 11, demonstrating that we achieve significant cooling with a small number of photons. The line corresponds to theory with Γm = 2π ⋅ 15 Hz. e shows an OMIT scan at the point of largest cooling Γeff with an effective linewidth Γeff ≈ 2π ⋅ 1.5 kHz, which corresponds to an effective four-wave cooperativity of \({{{{{{{{\mathcal{C}}}}}}}}}_{{{{{{{{\rm{fw}}}}}}}}}\gtrsim 100\). f shows the corresponding power-spectral density in units of quanta, displaying an asymmetric-noise lineshape due to a small, but finite effective temperature of the cavity by amplified quantum noise. Error bars in c consider uncertainties in the fitting procedure and in the bare mechanical linewidth, for details see Supplementary Note 14.

Full size image

The mechanical oscillator is well thermalized to the mixing chamber base temperature and its residual phonon occupation at the lowest operation temperature Tb = 15 mK is about \({n}_{{{{{{{{\rm{m}}}}}}}}}^{{{{{{{{\rm{th}}}}}}}}}\approx 70-90\) phonons, cf. inset of Fig. 4c. With increasing optical damping caused by the blue-detuned pump tone, we observe a corresponding reduction of the initial thermal occupation and the cooling factor is determined by Γopt, very similar to the usual optomechanical sideband cooling. The observed four-wave cooling is also very robust with respect to pump and drive strengths and we achieve at both flux bias operation points a final four-wave-cooled occupation extremely close to the quantum groundstate nm ~ 1.6. Due to the high single-photon coupling rates, it requires only a small amount of effective sideband photons nγ = ∣γ−∣2 + ∣γ+∣2 ≲ 10 to achieve these low occupations. A summary of these findings is presented in Fig. 4c–f.

The fact that we use strongly driven Kerr quasi-modes as cold bath, however, modifies the minimally achievable occupation. Due to Josephson parametric amplification of quantum noise in the quasi-mode state, the cavity will acquire an effective temperature, even if the bare cavity is in the quantum groundstate. This drive-induced cavity heating defines the cooling limit for the mechanical resonator. In the state we are operating here, the Josephson gain is small and the effective thermal occupation of the cavity is still considerably below 1. We estimate the current cooling limit due to amplified quantum noise to be ~0.6, where the exact value depends on the drive strength nd and on the bias-flux operation point. With higher bias-flux stability, the cavity could be stabilized at a point where the Josephson gain is small enough to enable \({n}_{{{{{{{{\rm{m}}}}}}}}}^{\lim } \, < \, 0.3\).

Achieving the lowest occupation in the current device requires a careful balancing of drive and pump strength, and for the highest pump powers, we observe the onset of additional cavity shifts and line broadening, possibly related to drive depletion or higher-order nonlinear effects. With slightly optimized device parameters regarding \({{{{{{{\mathcal{K}}}}}}}}\) and g0, we should therefore be able to cool to nm < 1. We emphasize though, that the blue-detuned cooling scheme allowed to achieve a significantly lower phonon occupation than signal-mode red-sideband pumping. With a pump on the red signal-mode sideband, a second cavity-bifurcation instability occurs at moderately high pump powers, as the red-sideband pump is attracting the cavity, while the blue-detuned pump is repelling it. The related jump to a high-amplitude state with a different signal resonance frequency, prevents us from cooling below \({n}_{{{{{{{{\rm{m}}}}}}}}}^{{{{{{{{\rm{red}}}}}}}}} \sim 5\). The corresponding red-sideband cooling data and analysis can be found in Supplementary Note 16.

Conclusions

The results we presented here demonstrate clearly that the young field of flux-mediated optomechanics is quickly advancing toward an exciting and competitive optomechanical platform, which intrinsically allows for novel ways of manipulating mechanical motion. Our device provides a large single-photon coupling rate of up to g0 = 2π ⋅ 3.6 kHz and achieves large cooperativities of up to \({{{{{{{{\mathcal{C}}}}}}}}}_{{{{{{{{\rm{fw}}}}}}}}}\, > \, 100\) for small numbers of intracavity photons. By using strong parametric driving, we show how the intrinsic Josephson-based Kerr nonlinearity can be utilized as a resource for improved sideband resolution, for the generation of frequency stability by an internal feedback-locking scheme, and for the implementation of a four-wave mixing-based phonon-control scheme. In combination, these properties enabled us to use four-wave cooling in a Kerr cavity to prepare a MHz mechanical nanobeam resonator close to its quantum groundstate. While implemented here using a SQUID cavity, we note that both of these techniques could be applied to any system with a Kerr nonlinearity, also in the case where flux-mediated optomechanics is not employed.

Future device improvements can be achieved by reducing the SQUID loop inductance further in order to increase the flux responsivity and the single-photon coupling rate. One order of magnitude is a feasible goal in this direction, as related platforms have already demonstrated such high responsivities16,17. This improvement alone would bring the device to a cooperativity of 104 and to the onset of the strong-coupling regime with g ~ 2π ⋅ 150 kHz ~ κ/2. With increased in-plane fields, up to ~1 T using, e.g., niobium or granular aluminum, those numbers could be improved by another order of magnitude.

In the current device, however, the main limiting factor that prevented us from achieving higher coupling rates and from cooling the mechanical oscillator into the groundstate was external flux noise coupling into the SQUID in large in-plane fields. We suspect that the origin of this flux noise is in the vector-magnet leads and the used current sources, respectively, or in parasitic out-of-plane components that lead to flux instabilities, vortex avalanches, and microwave-triggered vortex motion in proximity to the SQUID. Flux noise in the leads and current sources could potentially be reduced by using a superconducting magnet in persistent current mode. Although our current setup can locally cancel parasitic out-of-plane fields, it cannot do so over the complete chip simultaneously due to the geometry of the small coil. A global compensation might be necessary, however, to completely avoid any flux instabilities arising from the out-of-plane fields, which can cause flux fluctuations also in large distances from their occurrence. The demands for flux-noise suppression, however, are significantly relaxed by the presented stabilization mechanism.

Using intrinsic Kerr nonlinearities as a resource in optomechanical systems has just begun. Further interesting directions in Kerr optomechanics might involve intracavity squeezing, intracavity Josephson parametric amplification39, intracavity cat-state generation40, groundstate cooling in the sideband-unresolved regime, or enhanced quantum transduction31. Significantly larger Kerr nonlinearities than the ones presented here, implemented in superconducting transmon qubits, have also been discussed recently for mechanical quantum-state preparation24,41,42. Similar schemes investigating and exploiting the Kerr nonlinearity of SQUID circuits could furthermore be implemented naturally in the platform of photon-pressure-coupled circuits43,44,45. Therefore, we believe that Kerr optomechanics will constitute an extremely versatile and exciting platform for the preparation and investigation of mechanical quantum states and for optomechanical quantum technologies.

Methods

Sample fabrication

The first fabrication step is the petterning and deposition of the constriction-type Josephson junctions (cJJs). The resist patterning is done using electron beam lithography (EBL), followed by the DC magnetron sputtering of a 15-nm-thick layer of Al (1% Si) and liftoff in Anisole. In this first layer, we structure the narrow constrictions (~100 nm-long and ~50-nm wide) together with two ~1 μm2 large contact pads at each junction for a good galvanic contact to the rest of the circuit deposited in the second step. In the second step, all the remaining circuit is patterned using EBL again and an ~70-nm-thick Al (1% Si) layer is deposited, followed again by liftoff in Anisole. Directly before the sputter deposition, an in situ Ar-ion milling step is performed to remove the native oxide layer on top of the cJJ contact pads in order to achieve a low-loss galvanic contact between the layers. After testing the samples at this stage in a dilution refrigerator, we apply another well-timed Ar-ion milling process to the SQUID (the rest of the sample is covered in EBL-patterned resist) to finetune/reduce the critical currents of the junctions in order to achieve a good balance between screening parameter βL and the Kerr nonlinearity \({{{{{{{\mathcal{K}}}}}}}}\). The mechanical oscillator part of the SQUID loop is released in the last major fabrication step by EBL patterning a release window next to the SQUID loop into a fourth resist layer and exposing the sample to an isotropic reactive-ion etching process in SF6 plasma. The remaining resist after this step is removed by O2 plasma ashing. Finally, the sample is glued and wirebonded into a microwave printed-circuit board and mounted into the magnet body as shown in Fig. 1 A, more detailed description and a schematic of the fabrication process are given in Supplementary Note 1.

Experimental setup

Figure 1 shows photographs of the sample mounted on the PCB and fixed in the vector magnet bobbin. The two large parallel coils on each side of the sample are wound from a single wire (niobium–titanium in copper–nickel matrix) and in the same orientation and therefore form a Helmholtz-like split coil (the distance between the coils is slightly larger than their effective radius), which creates a nearly homogeneous in-plane magnetic field at the location of the device. The coil has approximately 2000 windings of superconducting wire on each side. From the coil geometry and the number of windings, we estimate the current-to-field conversion factor to be 70 mT/A. On the backside of the sample/PCB platform within the magnet bobbin is a second small coil mounted for providing the out-of-plane magnetic field used to tune the SQUID flux-bias point. This out-of-plane coil can also be used to compensate for a parasitic out-of-plane component of the in-plane field due to misalignments of the sample/PCB with respect to the in-plane field axis (estimated to be around 2∘–3∘ from the SQUID flux response). For in-plane fields B∥ ≲ 25 mT, however, the compensation is not yet critical. For larger in-plane fields, vortices start to penetrate the film and there is a dramatic reduction in the cavity quality factor observable. The out-of-plane coil has approximately 400 turns of superconducting wire and to a conversion factor of 1 mT/A. The superconducting wires leading to each of the coils from the 3-K plate are twisted in pairs, in order to reduce the amount of captured flux noise. Furthermore, since the critical temperature of the wire is about ~12 K, the wires can go unbroken until the 3-K stage. Above this plate, the wires are no longer superconducting and therefore a transition to normal conducting wires is required. For this, we connected each of the superconducting in-plane coil wires to 9 wires of a 24-line copper loom provided by Bluefors and each of the out-of-plane coil wires to 3 wires of the loom. From the 3-K stage until room temperature the current flows in parallel through the respective loom wires, decreasing the additional heat load on the plate. With this approach, we are able to send I∥ ~ 0.5 A through the in-plane coil without any considerable heat added to any of the plates and maintaining the fridge base temperature. At room temperature, we are left with 4 cables, two for each coil, which are used with individual directed current (DC) sources to independently generate the magnetic fields.

The experiments reported in this paper were performed in a dilution refrigerator with a base temperature Tb ≈ 15 mK. Within the outer vacuum can of the system, a mu-metal shield is installed to provide basic magnetic shielding for the whole sample space from the 3 K plate to the mK plate. A schematic diagram of the experimental setup and of the external measurement configuration used in the reported experiments can be seen in Supplementary Note 2. The PCB, onto which the fabricated sample is glued and wirebonded, is mounted into the magnet casing and connected to two coaxial lines. The complete configuration, including the vector magnet, is placed in a magnetic cryoperm shield. Since the optomechanical circuit that we present in this paper is designed in a side-coupled geometry, the input and output signals were sent/received through separate coaxial lines in order to measure the transmission spectrum of the feedline to which the system is coupled. The input line is heavily attenuated in order to balance the thermal radiation from the line to the base temperature of the fridge and the output line contains a cryogenic HEMT (high-electron-mobility transistor) amplifier working in a range from 4 to 8 GHz and two isolators to block the thermal radiation from the HEMT to reach the sample. Outside of the refrigerator, we used a single-measurement scheme for all the different experiments. The VNA was used to measure the response spectrum S21 of the electromechanical system, one microwave generator sends a coherent signal at ωd as parametric drive for the SQUID cavity and the second microwave generator sends a tone at ωp as optomechanical pump for the parametrically driven cavity. Finally, a spectrum analyzer was used to record the output power spectrum around the cavity resonance. For all experiments, the microwave sources and vector-network analyzers (VNA) as well as the spectrum analyzer used a single reference clock of one of the devices.