Introduction

Solid atomic hydrogen was postulated to be a high-temperature superconductor at high pressures by Ashcroft in 19681. Later, this idea has been revised and hydrogen-rich compounds have been hypothesized to be high-temperature superconductors at pressures that are only a fraction of the one needed to get atomic hydrogen2,3. The first experimental verification of that idea came in 2015 when H3S was shown to have a transition temperature of 203 K at 155 GPa4. This has been followed up by numerous experiments on different hydrogen compounds, many of them exhibiting high-temperature superconductivity5,6,7,8,9,10,11, verifying without a reasonable doubt the existence of superconductivity in hydrides at high pressures12.

The discovery of high-temperature superconductivity renewed the interest in synthesizing atomic metallic hydrogen, which is expected to superconduct above room temperature13,14,15,16. Recently, a work reported atomic metallic hydrogen at 495 GPa on the basis of enhanced optical reflectivity17. While this finding was questioned18 due to a probable overestimation of the measured pressure, there is an abundant amount of proof of finite electrical conductivity of solid hydrogen in the molecular phase19,20. None of these works, however, observed the transition to the superconducting phase up to 440 GPa. Many first-principles calculations predict the onset of superconductivity in solid hydrogen at significantly lower pressures21,22,23. The disagreement with experiments, in this case, is surprising in light of the success of the first-principles approach to superconductivity in other high-pressure hydrides3,24,25.

A better understanding of the high-pressure solid hydrogen phase diagram was provided by recent first-principles calculations considering both electronic correlations beyond density functional theory (DFT) and nuclear quantum effects26,27,28. Monacelli et al. show that at pressures lower than 422 GPa hydrogen crystallizes in the C2/c-24 phase, with 24 atoms in the primitive unit cell (phase III of solid hydrogen). In a pressure range between 422 and 577 GPa hydrogen transforms to the Cmca-12 phase, with 12 atoms per unit cell (phase VI). The value of 422 GPa agrees very well with the experimental transition pressures detected by infrared at 420 GPa20 and by Raman at 440 GPa19. Finally, at pressures higher than 577 GPa, hydrogen transforms into atomic hydrogen with a tetragonal I41/amd− 2 structure, containing two atoms per primitive unit cell.

One of the key reasons why studies in refs. 26,27 were able to successfully model the phase diagram of solid hydrogen was the inclusion of quantum anharmonic effects. The phonon renormalization due to anharmonicity can significantly alter superconductivity, as shown in refs. 21,22,25,29,30. However, these studies have not explored the anharmonicity-induced dynamical renormalization of phonons and its impact on superconductivity. Some studies have highlighted the importance of these effects on superconductivity utilizing simple single phonon mode toy models31,32. On the other hand, dynamical renormalization of phonons due to electron-phonon coupling has been shown to have little impact on the critical temperature33 of conventional superconductors. However, the dynamical effects due to phonon-phonon interaction should be much stronger in high-pressure hydrides, and thus, a full first principle study of these effects is necessary.

Here, we present a first-principles study of the superconducting properties of solid hydrogen in its high-pressure phases from 300 to 600 GPa by accounting for quantum anharmonic effects both on the phonons and the structure with the self-consistent harmonic approximation (SSCHA) at zero Kelvin. On top of the static renormalization of phonons (first-order perturbation theory terms of all anharmonic orders), we additionally include the dynamical renormalization of phonon quasiparticles (see Supplementary Note 4). We find that the SSCHA appreciably changes the structure of solid hydrogen in all phases, which leads to an increased density of states (DOS) at the Fermi level and an overall phonon softening. These two effects combine to increase the electron-phonon coupling constants and superconducting transition temperatures in the SSCHA structures, at odds with previous calculations that neglect the impact of ionic quantum effects on the structure21,22. We also show that the phonon spectral functions of all these phases have a complex and broad shape, clearly deviating from a simple Lorentzian, questioning the standard approximation made in the electron-phonon calculations in which the spectral function is represented with a Dirac delta function. By considering the full phonon spectral function, we show that the critical temperature (TC) of both molecular and atomic phases is considerably enhanced. Our calculations predict the onset of superconductivity in solid hydrogen in the semimetallic molecular phase VI at pressures between 450 and 500 GPa, which is consistent with recent experiments19, which did not observe superconductivity below 450 GPa.

Results and discussion

Quantum anharmonic effects have a large impact on the structures in the phase diagram, as shown in Fig. 1 (solid lines), compared to the structures that are minima of the Born-Oppenheimer energy surface (BOES) (dashed lines). There is a discontinuity in volume at the phase transition between molecular and atomic phases, not evident for the transition between molecular phases III and VI. This discontinuity is partly suppressed in the quantum anharmonic SSCHA structures. The SSCHA expands the structure slightly for all phases, most prominently for the atomic phase, increasing bond lengths and the c/a ratio at all pressures, as it has already been calculated in other high-pressure hydrides23,34. Importantly, SSCHA changes the qualitative behavior of bond lengths in molecular phases: while in SSCHA the bond length increases with pressure, in the classical harmonic approximation, in which it is determined by the minimum of the BOES, it stays relatively constant26.

Fig. 1: Structural, vibrational, and electronic properties of solid hydrogen with pressure.
figure 1

a Volume of the primitive unit cell per hydrogen atom, b length of the hydrogen-hydrogen bond, c the electronic density of states (DOS) at the Fermi level per hydrogen atom, and d the average phonon frequency in high-pressure solid hydrogen. Solid lines represent data obtained for structures relaxed within the stochastic self-consistent harmonic approximation (SSCHA) considering quantum anharmonic effects and dashed lines are for the structures that are minima of the Born–Oppenheimer energy surface. The color background shows a phase diagram of the solid hydrogen from ref. 27 and the color of the lines indicates for which phase calculations were performed.

Full size image

These changes have a significant effect on the electronic and vibrational properties of solid hydrogen (see Figs. 1 and 2 and Supplementary Note 1). The most prominent impact is the increase of the DOS at the Fermi level in the quantum anharmonic SSCHA structures. In the molecular phase VI, decreasing volume leads to an increase in the DOS, but with a considerably higher slope for the SSCHA structures than for the harmonic ones. This behavior shows that quantum anharmonic effects tend to increase the DOS at the Fermi level, as already described in several hydrides23,24. Molecular phase III is only weakly semimetallic up to 450 GPa and will not be discussed further on, as, thus, it cannot superconduct as suggested by the latest transport experimental results19. Closing of the fundamental band gap in our DFT calculations occurs above 400 GPa, which is slightly overestimated compared to calculations that include both better approximation for the exchange-correlation functional and the effect of the electron-phonon coupling26,28,35. The effects of the electron-phonon coupling (which is the main driver of the band gap closure) will be somewhat included in our superconductivity calculations through the self-consistent solution of Eliashberg equations.

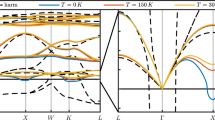
Fig. 2: Phonon spectral function of solid hydrogen.
figure 2

Phonon spectral functions in the no mode mixing approximation in mode basis, σμ(q, ω), of two representative optical phonon modes at Γ of solid hydrogen in a molecular Cmca-12 phase VI at 500 GPa, and b atomic tetragonal I41/amd-2 phase at 500 GPa. Thick dashed vertical lines represent the corresponding frequencies obtained from the auxiliary stochastic self-consistent harmonic approximation (SSCHA) force constants, while dotted lines represent the corresponding free energy Hessian frequency. In panel b we scaled the values of the Eg mode in order to make the figures clearer.

Full size image

In addition to the structure modified by quantum nuclear effects, the SSCHA method allows us to obtain auxiliary second-order force constants renormalized by anharmonicity. Quantum anharmonicity softens phonon frequencies as a consequence of the stretching of the H bonds (see Fig. 1). This is at odds with recent calculations21,22, in which the frequencies of the phonon modes excluding the vibrons increase due to anharmonicity. The difference is that, in the latter case, the effect of the quantum zero-point fluctuations on the structure was neglected, which our calculations show to be important. Additionally, in the SSCHA of ref. 22 a truncated potential is used (to the fourth order), which gives slightly different results compared to the SSCHA method where all anharmonic orders are included in the calculation of the auxiliary force constants. Both the increase of the DOS at the Fermi level and the phonon softening are beneficial for superconductivity since the electron-phonon coupling constant scales inversely with phonon frequencies and linearly with the DOS at the Fermi level.

Beyond the renormalization of structural parameters and phonon frequencies, anharmonicity has a huge impact on the phonon spectral function (see Supplementary Note 3). The spectral function of all phases shows further softening with respect to the auxiliary SSCHA phonon frequencies, especially for high-frequency optical modes. This softening can be also captured with the calculation of the free energy Hessian. Specifically, in the static limit, the peaks of the phonon spectral function coincide with the frequencies obtained diagonalizing the free energy Hessian. However, Fig. 2 clearly demonstrates the range of applicability of the free energy Hessian for describing vibrational properties. It is a good approximation in the vicinity of the vanishing imaginary self-energy, that is, when auxiliary SSCHA frequency is close to 0 or when there is no large broadening of the phonon spectral line.

In addition to the aforementioned softening, we predict a huge broadening of the phonon spectral functions of the order of thousands of cm−1 even at vanishing temperatures. In this case, phonon spectral functions clearly deviate from the standard Lorentzian line shape. We illustrate this in Fig. 2, where phonon spectral functions for selected modes at Γ point are presented for structures at 500 GPa in molecular phase VI and atomic phase. We report two representative modes for molecular phase VI: a global lattice vibration (phonon mode) and a stretching of H2 molecule (vibron mode). In the atomic phase, we only have two optical modes that are non-degenerate and we show both of them. The shift of the phonon frequency is very large in all cases. Additionally, all modes, except the Eg one in the atomic phase, have a huge broadening of the phonon spectral function of thousands of cm−1 and a clear non-Lorentzian line shape. Such anomalous behavior questions the standard practice of approximating the spectral function with slightly smeared Delta functions in first-principles calculations of the superconducting critical temperatures. In fact, it has already been shown that non-Lorentzian lineshapes can have a non-negligible effect on other properties of materials, i.e., the lattice thermal conductivity in highly anharmonic semiconducting chalcogenides36.

The isotropic Eliashberg function of the electron-phonon interaction can be calculated keeping the full anharmonic spectral function as37

$${\alpha }^{2}F(\omega )=\frac{1}{{N}_{{{{{{{{\bf{q}}}}}}}}}}{\sum}_{ab{{{{{{{\bf{q}}}}}}}}}\frac{{\Delta }^{ab}({{{{{{{\bf{q}}}}}}}}){\sigma }_{ab}({{{{{{{\bf{q}}}}}}}},\omega )}{\omega \sqrt{{m}_{a}{m}_{b}}},$$
(1)

where σab(q, ω) is the phonon spectral function in the Cartesian basis with wave number q (see Supplementary Note 4). In Eq. (1) a and b label both atoms in a Cartesian direction, Δab(q) represents the average of the deformation potential over the Fermi surface, ma is the mass of atom a, and Nq is the number of q points in the sum. In the harmonic case, α2F(ω) is calculated for the structure that minimizes the BOES, while in the SSCHA it is calculated for the structure that minimizes the free energy. Eq. (1) offers a straightforward approach to studying the impact of anomalous phonon lineshapes into superconducting properties. However, Δab(q) includes only the linear term in the electron-phonon interaction without considering higher-order terms that may become important due to quantum nature of hydrogen ions and which are included in other approaches38,39.

All calculations thus far that have accounted for anharmonicity in the calculation of α2F(ω) have been performed assuming that σab(q, ω) can be expressed as15,23,24,25,29,30\({\sigma }_{ab}({{{{{{{\bf{q}}}}}}}},\omega )={\sum }_{\mu }{e}_{\mu }^{a}({{{{{{{\bf{q}}}}}}}}){e}_{\mu }^{b* }({{{{{{{\bf{q}}}}}}}}){\sigma }_{\mu }^{{{{{{{{\rm{h}}}}}}}}}({{{{{{{\bf{q}}}}}}}},\omega )\), where the harmonic spectral function \({\sigma }_{\mu }^{{{{{{{{\rm{h}}}}}}}}}({{{{{{{\bf{q}}}}}}}},\omega )\) of mode μ and wave number q is a Delta function centered at the harmonic or SSCHA auxiliary phonon frequency, and eμ(q) are either harmonic or SSCHA phonon eigenvectors. As in practical implementations, the Delta functions are numerically approximated with a Gaussian function of fixed spread, we label this approach as Gaussian. However, as we have shown in Fig. 2, anharmonicity can drastically affect the phonon lineshapes. In order to obtain σab(q, ω), here we utilize the full phonon spectral function. In this case, we do not assume that the phonon self-energy is diagonal in the phonon branch index, as it is usually done, and instead calculate the spectral function as \({\sigma }_{ab}({{{{{{{\bf{q}}}}}}}},\omega )={\sum }_{\mu \nu }{e}_{\mu }^{a}({{{{{{{\bf{q}}}}}}}}){e}_{\nu }^{b* }({{{{{{{\bf{q}}}}}}}}){\sigma }_{\mu \nu }({{{{{{{\bf{q}}}}}}}},\omega )\) fully accounting for off-diagonal terms in phonon self-energy. Here, the polarization vectors are obtained from the SSCHA auxiliary dynamical matrices. Including full phonon spectral functions drastically changes the calculated α2F(ω), as shown in Fig. 3. The previously mentioned softening of the phonon modes is also evident in the Eliashberg spectral functions. Additionally, the broadening of the phonon lineshapes leads to the complete closing of the gap between hydrogen vibron and phonon branches in the molecular phase VI. The softening of the phonon modes in the SSCHA coupled with a higher DOS at the Fermi level in the SSCHA structures leads to higher values of the electron–phonon coupling constant λ in most cases compared to the harmonic result, more remarkably in the molecular phase VI (see Fig. 3a and Supplementary Note 4). A notable exception is atomic hydrogen at 500 GPa (depicted in Fig. 3b), where the proximity to a phonon instability, which is suppressed by anharmonicity, drastically increases λ in the harmonic approximation. Finally, it is worth noting that the no-mode-mixing approximation (treating phonon self-energy as diagonal in phonon branches), which is more commonly used for the calculation of phonon spectral functions, yields similar results to those obtained with the full off-diagonal spectral function.

Fig. 3: Eliashberg spectral function α2F(ω) and integrated electron-phonon coupling constant λ(ω) of solid hydrogen.
figure 3

Eliashberg spectral function α2F(ω) and integrated electron-phonon coupling constant λ(ω) of solid hydrogen in a molecular Cmca-12 phase VI at 500 GPa, and b atomic tetragonal I41/amd − 2 phase at 500 GPa. The Gaussian-Harmonic label refers to results calculated with harmonic phonons of the DFT structures in the Gaussian approximation for the phonon spectral function. Gaussian-Hessian refers to results calculated with phonons from free energy Hessian calculated for the stochastic self-consistent harmonic approximation (SSCHA) structures in the Gaussian approximation for phonon spectral function. Finally, Full results were obtained for SSCHA structures with the α2F calculated with the full phonon spectral function matrix. Legend in panel b applies for a as well.

Full size image

Solving isotropic Migdal-Eliashberg equations with the α2F(ω) obtained considering the full spectral function37,40, we can estimate the impact of anharmonicity on the superconducting transition temperature (see Fig. 4). As mentioned above, the C2/c−24 phase of solid hydrogen does not exhibit superconducting behavior in the pressure range of interest. In the molecular phase VI, the transition temperature is mostly linear with pressure and correlates well with the value of the DOS at the Fermi level. Because of this, the SSCHA structures consistently show higher transition temperatures than the classical harmonic ones. The difference in TC between these two methods increases with pressure, again due to the stronger dependence of the electronic DOS on the pressure in the SSCHA structures (see Fig. 1), as well as due to the increased electron-phonon coupling due to the anharmonic softening of the phonon modes.

The estimate of the superconducting transition temperature obtained utilizing full phonon spectral function in all cases is larger than the one obtained using auxiliary SSCHA force constants and Gaussian approximation by ~30 K. On the other hand, Gaussian approximation coupled with the phonons from the Hessian of the total free energy gives a larger critical temperature than the full phonon spectral function calculation (at most 15 K). Since Hessian calculations only incorporate the softening of the phonon modes, the conclusion is that the softening of phonon modes increases the critical temperature while the broadening of the phonon spectral lines reduces it. Considering that α2F(ω) is intimately related to the electron self energy37 we can assume that the phonon spectral functions will have an influence on other material properties that strongly depend on the electron self-energy, such as electrical conductivity, Seebeck coefficient, band gap renormalization, etc. We would like to highlight that at this moment, the effects of the finitely lived phonon quasiparticles are not accounted for in any first-principles calculations, while our results show they might have a large effect.

Fig. 4: Superconducting critical temperature in solid hydrogen.
figure 4

Calculated superconducting transition temperature in solid hydrogen in different phases and pressures within the stochastic self-consistent harmonic approximation (SSCHA) using the full phonon spectral functions (full symbols and solid lines) and the harmonic approximation using the Gaussian method (empty symbols and dashed lines). Shaded regions represent the phase diagram of solid hydrogen from ref. 27. Line colors denote for which phase calculations were performed (red for molecular phase VI and purple for atomic phase).

Full size image

Considering the critical dependence of TC on the DOS at the Fermi level and that local exchange-correlation functionals tend to overestimate it13,15,21,22,41,42, we perform DFT calculations for the quantum SSCHA structures of phase VI using the B3LYP hybrid functional43 (see Supplementary Note 2). Since the critical temperature correlates linearly with the electronic DOS in the Cmca-12 phase, we can estimate the superconducting transition temperature using the DOS from the better B3LYP calculation. With this procedure, we predict that superconductivity will emerge in solid hydrogen in the Cmca-12 phase between 450 and 500 GPa. This result is consistent with a recent experiment19, which failed to observe superconductivity at 440 GPa in what was identified as a molecular phase VI26.

In the atomic tetragonal phase, the critical temperature is mostly constant with pressure. In this phase, TC is mostly decorrelated with the value of the electronic DOS at the Fermi level because the structures are far away from the metal-insulator phase transition27 and, despite quantum and anharmonic effects enhancing the DOS as well, its relative increase is small compared to the molecular case. Accounting for the full phonon spectral function in the calculation of α2F(ω) increases the estimate of the critical temperature by 20 K compared to the case using the Gaussian approximation and SSCHA auxiliary force constants (see Supplementary Note 4). This increase is much larger than the one induced by the SSCHA structure renormalization (<5 K away from the structural instabilities, see Supplementary Note 4). This highlights the important role that anharmonicity plays in the superconductivity of high-pressure hydrogen also in the atomic phase, contrary to the previous calculations that only estimated its effect within the Gaussian approximation of the spectral function15.

In conclusion, our first-principles calculations considering ionic quantum effects and anharmonicity show that superconductivity will emerge in solid hydrogen in molecular phase VI, between 450 and 500 GPa, and TC will rapidly soar with pressure. We expect a jump of TC to ~350 K at the transition to the atomic phase. Quantum anharmonic effects have a huge impact on the structural, vibrational, and superconducting properties of both molecular and atomic phases by, for instance, increasing the H-H bonds and making the phonon spectral functions extremely broad and anomalous. We show that considering the full phonon spectral function in the calculation of α2F(ω) enhances the predicted critical temperature by 25 K in the atomic phase and 30 K in the molecular phase VI.

Methods

DFT and density functional perturbation theory (DFPT)44 calculations were performed using Quantum Espresso software45,46, implementing the generalized gradient approximation (GGA) with the BLYP parameterization47 for the exchange-correlation functional. In the case of the primitive unit cell calculations, we used a Monkhorst-Pack grid for sampling electronic states with densities of 48 × 48 × 48 for the atomic phase, 12 × 12 × 12 for the molecular phase VI, and 12 × 6 × 12 for molecular phase III. The electronic wave functions were represented in a plane wave expansion using an 80 Ry energy cutoff (320 Ry cutoff for the electronic density). To describe hydrogen ions, we used a norm-conserving pseudopotential with no pseudized electrons generated by the Pseudo Dojo library48 and the ONCVPSP software49. Considering that we are investigating metallic/semimetallic phases we used a Marzari-Vanderbilt smearing of 0.03 Ry50 for Brillouin zone integrations.

To get the structural and vibrational properties of solid hydrogen we used the stochastic self-consistent harmonic approximation (SSCHA). The SSCHA method51,52,53,54 allows us to minimize the total free energy of the system, which includes the quantum zero-point motion and anharmonicity, with respect to two variational parameters that define the ionic wave function: the centroid positions and the auxiliary force constants. The centroids are the average positions of the atoms (the means of the Gaussians that approximate the ionic wave functions). The auxiliary force constants are related to the standard deviation of the Gaussians. Eigenvalues of the dynamical matrices constructed from these auxiliary force constants can be regarded as better estimates of the true phonon frequencies than the simple harmonic force constants since they have been renormalized by anharmonicity. More precisely, in perturbation theory language these force constants include contributions to the first order in perturbative expansion from all of the anharmonic terms in the expansion of the BOES. These corrections are purely real and only shift the phonon frequency. The centroids and SSCHA auxiliary second-order force constants are obtained at the end of the minimization of the total free energy. Additionally, on top of renormalizing the second-order force constants, SSCHA renormalizes the anharmonic force constants as well in a similar manner.

From here, we can go a step further and include some terms of the higher orders in the perturbation theory that stem from third and fourth-order anharmonic force constants (renormalized by anharmonicity as explained above), which are consistent with SSCHA54,55,56,57. The phonon Green’s function (\({G}_{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}},\omega )\)) in this case can be expressed as:

$${G}_{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}},\Omega )={\left[{\Omega }^{2}{\delta }_{\mu {\mu }^{{\prime} }}-{{D}^{(2)}}_{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}})-{\Pi }_{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}},\Omega )\right]}^{-1}.$$

Here \({{D}^{(2)}}_{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}})\) is the dynamical matrix constructed from the SSCHA auxiliary force constants and \({\Pi }_{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}},\omega )\) is phonon self-energy that depends on the SSCHA anharmonic force constants (\({{{{{{{{\bf{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}}^{(3)}({{{{{{{\bf{q}}}}}}}}),{{{{{{{{\bf{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}}^{(4)}({{{{{{{\bf{q}}}}}}}})\)):

$${{{{{{{\mathbf{\Pi }}}}}}}}({{{{{{{\bf{q}}}}}}}},\Omega )={{{{{{{{\bf{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}}^{(3)}({{{{{{{\bf{q}}}}}}}}):{{{{{{{\mathbf{\Lambda }}}}}}}}({{{{{{{\bf{q}}}}}}}},\Omega ):{\left[{{{{{{{\bf{1}}}}}}}}-{{{{{{{{\bf{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}}^{(4)}({{{{{{{\bf{q}}}}}}}}):{{{{{{{\mathbf{\Lambda }}}}}}}}({{{{{{{\bf{q}}}}}}}},\Omega )\right]}^{-1}:{{{{{{{{\bf{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}}^{(3)}({{{{{{{\bf{q}}}}}}}}).$$

The double-dot product X:Y indicates the contraction of the last two indices of X with the first two indices of Y. If we denote the eigenvalues of the SSCHA auxiliary dynamical matrices as ωμ(q) and associated Bose-Einstein factors as nμ(q), the above Λ(q, Ω) is given as:

$${\Lambda }^{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}},\Omega ) = \frac{1}{4{\omega }_{\mu }({{{{{{{\bf{q}}}}}}}}){\omega }_{{\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}})}\left[\frac{\left({\omega }_{\mu }({{{{{{{\bf{q}}}}}}}})-{\omega }_{{\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}})\right)\left({n}_{\mu }({{{{{{{\bf{q}}}}}}}})-{n}_{{\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}})\right)}{{({\omega }_{\mu }({{{{{{{\bf{q}}}}}}}})-{\omega }_{{\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}}))}^{2}-{\Omega }^{2}+i\epsilon } \right. \\ \left. -\frac{({\omega }_{\mu }({{{{{{{\bf{q}}}}}}}})+{\omega }_{{\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}}))(1+{n}_{\mu }({{{{{{{\bf{q}}}}}}}})+{n}_{{\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}}))}{{({\omega }_{\mu }({{{{{{{\bf{q}}}}}}}})+{\omega }_{{\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}}))}^{2}-{\Omega }^{2}+i\epsilon }\right].$$
(2)

\({\Pi }_{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}},\omega )\) is not purely real and describes the realistic broadening of the phonon spectral functions. However, in the static limit (Ω→0), the contributions from these terms are again only real and can be included to further renormalize the SSCHA second-order auxiliary force constants. Force constants obtained in this manner are Hessians of the total free energy, \({G}_{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}},0)\). If any of the eigenvalues of the Hessian of the total free energy is negative, the structure is unstable. These force constants can alternatively be used to describe the vibrational properties of the material. In the static limit, for the calculation of the Hessian of total free energy, we include the contributions of both the third and fourth-order SSCHA anharmonic force constants.

However, a physically more relevant representation of the vibrational properties of materials comes from the phonon spectral functions obtained in the dynamical dressed-bubble approximation, using auxiliary force constants and third-order force constants from SSCHA as described in refs. 54,55,56,57:

$${\sigma }_{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}},\Omega )=-\frac{\Omega }{\pi }{{{{{{{\rm{Im}}}}}}}}{G}_{\mu {\mu }^{{\prime} }}({{{{{{{\bf{q}}}}}}}},\Omega ).$$

The anharmonicity, in general, leads to the mixing of the phonon modes, and the matrices of phonon spectral functions at different values of the frequency (energy) Ω do not commute. Usually, this is disregarded, and only the diagonal part \(\mu ={\mu }^{{\prime} }\) of the phonon spectral function (in the space of eigenvectors that diagonalize auxiliary SSCHA force constants) is taken into account. This approximation is referred to as a no-mode-mixing approximation in this work. Alternatively, one can use the true phonon spectral function, including the off-diagonal terms in the phonon spectral functions, and that approach is termed full in this work.

The sampling of atomic positions and forces for SSCHA calculations was done on a 5 × 5 × 5 primitive cell repetition for the atomic phase, 2 × 2 × 2 for the molecular phase VI, and 2 × 1 × 2 for the molecular phase III. The number of configurations used for the stochastic sampling was 500 for the atomic phase, 600 for molecular phase VI, and 6000 for molecular phase III. To calculate third-order force constants needed to calculate the spectral functions, we used a finer stochastic sampling of 3000 structures for the atomic phase and 20000 structures for phase VI. SSCHA calculations were performed at 0 K. For the calculation of the phonon spectral functions we used the dynamical bubble term in the phonon self-energy expansion. In the static limit, the peaks of the phonon spectral function coincide with the frequencies obtained from the free energy Hessian. For the Hessian calculations, in the molecular phase, we used the static bubble term from the third-order anharmonicity and fourth-order anharmonicity double bubble term, and for the atomic phase, we used only the third-order static bubble term. The SSCHA auxiliary force constants already include the effects of so-called tadpole and loop terms, as well as higher orders of anharmonicity.

Finally, we performed a convergence study of the electron-phonon coupling constant and the critical temperature with respect to the q point grid in DFPT calculations. We have found that reasonably converged results were obtained with a 12 × 12 × 12 q point grid for the atomic phase, 8 × 8 × 8 for phase VI, and 8 × 4 × 8 for phase III (see Supplementary Note 5). The calculated electron-phonon coupling constants from DFPT were projected onto SSCHA phonon modes25. k-point grids for the non-self-consistent calculations for the electron-phonon coupling were done on 100 × 100 × 100 grids for the atomic phase, 44 × 44 × 44 for phase VI, and 44 × 22 × 44 for phase III with Gaussian smearing of 0.012 Ry for the energy conservation Dirac deltas. Finally, to calculate superconducting transition temperatures, we used the isotropic approximation of the Migdal-Eliashberg (ME) equations in the constant DOS approximation37. We use μ* = 0.16 for the Coulomb pseudopotential and a cutoff for the Matsubara frequencies of 10 times the highest phonon frequency37. We have checked that this approximated approach to solving ME equations yields accurate results despite the use of the μ* parameter. For example, in LaH10, where superconductivity is dominated by the hydrogen sublattice, this approach only yields an overestimation of TC of 7% with respect to anisotropic ME equations and the use of the random phase approximation to calculate the Coulomb repulsion (to avoid the use of the simple μ* parameter)24,58.