A computational topology-based spatiotemporal analysis technique for honeybee aggregation

Abstract

A primary challenge in understanding collective behavior is characterizing the spatiotemporal dynamics of the group. We employ topological data analysis to explore the structure of honeybee aggregations that form during trophallaxis, which is the direct exchange of food among nestmates. From the positions of individual bees, we build topological summaries called CROCKER matrices to track the morphology of the group as a function of scale and time. Each column of a CROCKER matrix records the number of topological features, such as the number of components or holes, that exist in the data for a range of analysis scales, at a given point in time. To detect important changes in the morphology of the group from this information, we first apply dimensionality reduction techniques to these matrices and then use classic clustering and change-point detection algorithms on the resulting scalar data. A test of this methodology on synthetic data from an agent-based model of honeybees and their trophallaxis behavior shows two distinct phases: a dispersed phase that occurs before food is introduced, followed by a food-exchange phase during which aggregations form. We then move to laboratory data, successfully detecting the same two phases across multiple experiments. Interestingly, our method reveals an additional phase change towards the end of the experiments, suggesting the possibility of another dispersed phase that follows the food-exchange phase.

Introduction

The sophisticated social organization among honeybees (Apis mellifera L.) involves intricate interaction networks that are critical to the function of the hive. One important example is the exchange of food among colony members, which is performed through a process called trophallaxis¹, a mutual feeding technique that involves the direct transfer of liquid food among nestmates. Trophallaxis interactions cause aggregations to form in the group², as shown in Fig. 1b. Analysis of these patterns can help us understand how this collective food-exchange network evolves over time, which can in turn provide valuable information about the efficiency of global food distribution among honeybees.

Fig. 1: Trophallaxis in honeybees. In this experiment, a number of fed donor bees are introduced into a larger group of food-deprived bees, at which point they begin exchanging food and forming aggregations.

a Shows the situation at the beginning of the experiment (t = 0), before the introduction of the donor bees at t = 430 s. b Shows aggregations that have formed by t = 545, with an inset focusing on a donor bee (marked with a dot) and two receiver bees as they exchange food. The scale bar in panel b, which corresponds to 5 cm, also applies to panel a.

In this paper, we use topological data analysis (TDA) to perform a rigorous spatiotemporal analysis of the morphology of honeybee groups during the process of trophallaxis. TDA is a set of mathematical tools for characterizing the shape of real-world data. One of those tools, known as persistent homology³, takes a variable-resolution approach to the shape-analysis problem, treating points as connected if they are within some distance ϵ of one another and counting the number of topological features—connected components, two-dimensional holes, three-dimensional voids, etc.—in the resulting simplicial complex. By repeating that analysis for a range of values of the connectivity parameter ϵ, this method produces a rich, multi-scale signature of the spatial structure of a point cloud. This approach has grown in popularity for a variety of applications over the past decade, including a number of biology problems^{4,5,6,7,8,9,10}, but it has not yet been applied to honeybee groups, whose patterns have largely been studied using computer-vision techniques^2,11,12. These require a priori definitions of the specific scales at which aggregation occurs, however. TDA offers a reliable way to perform a detailed spatiotemporal analysis of the aggregations without any such assumptions.

Here, we use the tools of TDA to study honeybee aggregations in the context of trophallaxis, with a particular emphasis on discerning how these aggregations evolve over time. Our approach draws an analogy between changes in these patterns, termed “phase changes” in the rest of this document, and the density phase transitions observed in condensed matter^13,14,15. Notable density-related phases in this application encompass a sparse phase (where bees are uniformly distributed across the arena), a dense phase (where bees form a cohesive cluster), as well as various intermediate states characterized by combinations of dense and sparse clusters, such as the presence of multiple smaller clusters or the coexistence of dense and sparse configurations. In order to track the dynamical evolution of the topological signatures produced during our analysis of these changing patterns, we use the CROCKER method (Contour Realization Of Computed k-dimensional hole Evolution in the Rips complex), a matrix-based representation that captures the morphology of a point cloud as a function of both scale and time⁶. Each column of a CROCKER matrix corresponds to a particular time point in the experiment. The elements of that column vector record the number of topological features that exist in that data snapshot for a range of analysis scales—e.g., the number of ϵ-connected components for a range of values of the scale parameter ϵ. We use dimensionality reduction techniques to convert each of these vectors to a scalar, then use clustering algorithms to find the phase changes in the resulting time series.

In the following section, we describe our methods in more detail and apply them to a synthetic dataset from an agent-based model of trophallaxis in honeybees. In the “Applications to experimental data” section, we use this methodology to study trophallaxis in a laboratory experiment. In both simulated and real data, these methods clearly bring out the different phases in the behavior. We discuss some alternative approaches and implications of our findings in the “Discussion” section. Throughout this document, we use the term “aggregation” to describe a group of bees in physical space and the term “clustering” for the action of algorithms that find groups in the resulting structure.

Spatiotemporal TDA of honeybee aggregations

To demonstrate our method, we apply it to data that we generate using an agent-based model of trophallaxis that was first described in ref. ². To avoid repetition, we provide a concise summary of the simulation; please see ref. ² for more details. At the start of each run of this model, a number of bee-agents with zero values of a food-level variable are placed randomly in a 2D simulation arena, as depicted in Fig. 2a. As the simulation progresses, these agents perform random walks, remaining scattered around the arena. Partway through the simulation run, a number of donor bee-agents—with positive values of the food-level variable—are introduced into the arena. All agents continue moving via random walks, stopping to exchange food with one another if they come within a predefined attraction radius (2.5 simulation patches). The length of the food exchange, during which both agents remain stationary, is proportional to the difference between their food levels; at its end, the food levels are equalized between the two. During this process, aggregations form in the group, as shown in Fig. 2b, c, while the food is distributed across the agents. For this series of simulations, we end all model runs at t = 900.

Fig. 2: Snapshots from an agent-based model of trophallaxis.

a At the start of the simulation (t = 0), a 36 by 36 cell arena with reflective boundary conditions contains 38 food-deprived agents moving via random walk. b Agents at t = 650, after four donor bee-agents are introduced at t = 400, when aggregations form as the food carried by those agents is distributed across the group. c Another snapshot at t = 900. Agents are colored by their amount of food (zero food is shown in white and maximal food capacity is shown in red).

Note that the morphology of the group of agents cannot be simply classified as “aggregated” or “not-aggregated.” The structure in the three panels of Fig. 2, shows different degrees of aggregation; moreover, any classification as to the degree of aggregation will depend on what measure of proximity one uses to define membership in an aggregation. Topological data analysis is an effective way to quantify the multi-scale nature of this structure in an effective and formal way. As mentioned previously, persistent homology characterizes the shape of a data set by analyzing it at different resolutions. This involves building a filtration from the point cloud: a series of simplicial complexes that capture its structure for different values of a resolution parameter, ϵ. For this purpose, we use the Vietoris-Rips¹⁶ approach, which constructs a complex by creating balls of radius ϵ around each data point. A set of m points is connected by an m-simplex if every pair of points in the set has intersecting ϵ-balls. From each of the resulting series of simplicial complexes, one then computes the Betti numbers: β = {β₀, β₁, β₂, …. }, where β₀ is the number of connected components, β₁ is the number of two-dimensional loops, β₂ is the number of three-dimensional voids, and so on. Figure 3 shows an example of filtration: a series of simplicial complexes constructed from the data in Fig. 2b for six values of ϵ. The effects of the filtration parameter are clearly visible across the panels of the figure: for ϵ = 0, each agent is its own connected component—i.e., β₀ = 38, the number of agents in the simulation at that point in time—while for ϵ = 15 all agents are connected together in one connected component (β₀ = 1). In between those values, the component structure reflects the patterns in the spacing of the bees as the ϵ value grows to span larger and larger gaps between the individuals, connecting them in the Vietoris-Rips complex. Values for the other Betti numbers β_k can be similarly calculated for different ϵ values to produce a multi-scale topological signature of the point cloud.

Fig. 3: Vietoris-Rips complex.

A series of Vietoris-Rips complexes constructed from the positions of the bees in Fig. 2b for six values of the filtration parameter ϵ.

To carry out these calculations, one must specify the scales for the construction: specifically, the range $[{\epsilon }_{\min },\,{\epsilon }_{\max }]$ and spacing Δϵ of the filtration parameter. A common approach to choosing the range is to take ${\epsilon }_{\min }$ at the value where each point is its own component and ${\epsilon }_{\max }$ such that the entire set is connected. For the example in Fig. 3, this approach suggests $[{\epsilon }_{\min },\,{\epsilon }_{\max }]=[0,\,15]$. In other runs of the model, however, a higher ϵ was required to connect all the agents into a single component, so we standardize by using ${\epsilon }_{\max }=20$, which was adequate to produce ${\beta }_{0}({\epsilon }_{\max })=1$ for all time points in all model runs. Choosing the spacing, Δϵ, involves balancing computational complexity, analysis resolution, and the scales in the data. What one wants is a Δϵ that yields new information at each step: if it is too small, the filtration will contain multiple elements with identical topology; if it is too large, those elements may skip over ϵ values where important topological changes occur. To steer between these extremes, we calculate the average pairwise distances between bees in neighboring cells across every time point in every model run, obtaining a value of 1.41, and then take a somewhat smaller value, Δϵ = 1, to be sure not to miss important topological changes. This choice yields n = 21 simplicial complexes at each time point. Since we are interested in aggregations, we focus on the number of ϵ-connected components, β₀, in each of these complexes. This computation, which we perform with the GUDHI Python package^17,18, requires 62 μsec for each of the 21 complexes in the filtration (i.e., 0.0013 sec total for each time point) on an Apple M1 Pro with 10 CPU cores and 16GB of main memory.

From a data-analysis standpoint, the procedure described above can be viewed as converting a set of points into a n-vector [β₀(ϵ₀), β₀(ϵ₁), …β₀(ϵ_n)] that characterizes the shape of that point cloud for n different values [ϵ₁, ϵ₂, …, ϵ_n] of the resolution parameter. To detect phase changes in that structure, we need a way to track the evolution of that shape with time. Various representations have been proposed for that purpose, including CROCKER plots⁶, vineyards¹⁹, multiparameter rank functions²⁰, and CROCKER stacks²¹. In this paper, we use CROCKER plots, which are two-dimensional representations with time on the horizontal axis and information about scale and structure on the other. The columns of the matrices that are rendered by these plots are a series of vectors like the ones mentioned above, each of which records, for a given point in time t_i, the value of β₀ for each of n values of ϵ in the filtration:

$${\vec{b}}({t}_{i})={[{\beta }_{0}({t}_{i};{\epsilon }_{0}),{\beta }_{0}({t}_{i};{\epsilon }_{1}),\ldots {\beta }_{0}({t}_{i};{\epsilon }_{n})]}^{T}$$

(1)

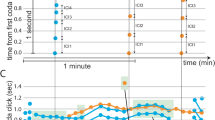
The plots themselves visualize this information using color-coded contours on the ${\vec{b}}$ values. Figure 4a shows an example: a CROCKER plot constructed from the bee positions in one run of the agent-based model. The dark blue region across the bottom of the image reflects the large number of ϵ-connected components that exist in the simplicial complex when ϵ is small; the contour that divides the yellow region from the light green region identifies the ϵ value at which the complex at the associated time point includes all of the points in the simulation. The plot reveals a clear shift in the topology soon after the introduction of the donor bees, where the contours change drastically around t = 400 s. Lower-valued contours (separating lighter sections) separate and raise slightly, and higher-valued contours fall and bunch together more closely. Overall, these changes mean that reduction from a large number of clusters to a moderate number, say from 42 to around 10, occurs at smaller scales than before. Conversely, reduction from moderate numbers of clusters to a single cluster occurs at larger scales than before. The latter case is consistent with bees forming small groups that are spaced throughout the domain.

Fig. 4: TDA analysis of the agent-based model.

a A CROCKER plot of the positions of the bees in an agent-based model run. The colors indicate the number of connected components (β₀) in the simplicial complex constructed with the ϵ value on the y-axis. The black box highlights a vertical slice of the CROCKER plot, ${\vec{b}}=[{\beta }_{0}({\epsilon }_{i})]$, at the corresponding time point. b A time series of the ℓ² norms of each of these ${\vec{b}}$ vectors, with superimposed lines for the results of the change-point detection algorithm, (dash-dotted blue line, at t = 415), and the two clustering algorithms: k-means (dotted pink line, at t = 415) and agglomerative (dashed orange line, at t = 427). The solid vertical black line at t = 400 indicates when the fed agents are introduced into the model.

This shift in the patterns confirms previous results cited in the section “Introduction” about the ability of CROCKER plots to make phase changes in biological aggregations visually apparent. Our present goal is to go beyond visual observations and develop formal methods for detecting those phase changes automatically. We evaluate two different types of algorithms for the associated calculations:

• A standard change-point detection algorithm: recursive binary segmentation of the time series, based on a likelihood ratio test.

• Two unsupervised clustering algorithms—k-means and agglomerative^22,23—which are representative of this class of methods.

The basic idea is to apply these algorithms to the column vectors ${\vec{b}}(t)$ in the CROCKER matrix. If the vectors before and after the introduction of the donor bees do indeed capture some distinct morphology, the algorithms should separate them into two separate regimes, effectively resulting in a phase change detection. The column vectors require some pre-processing before these algorithms can be applied, however. Their high dimensionality, coupled with the comparatively short number of time points in each phase, can make it difficult to run clustering algorithms, and the change-point detection algorithm requires a scalar input. To work around this, we apply dimensionality reduction techniques to the column vectors and then run the phase change detection algorithms on the resulting low-dimensional time series. A simple way to do this is to take the ℓ² norms of each ${\vec{b}}(t)$. The results of this procedure, applied to the CROCKER matrix plotted in Fig. 4a, are shown in Fig. 4b. There is a clear shift in the normed values at the time of the change in structure of the CROCKER plot after the introduction of the donor bees.

To isolate this shift, we apply the three different algorithms to this scalar time series, with the goal of identifying the time t_shift at which the structure changes. In the k-means algorithm, the user must specify how many clusters (k) to search for. Since we are looking for two distinct phases in the ${\vec{b}}$ vectors, we choose k = 2. The algorithm begins by randomly mapping each vector in the dataset to one of the k clusters, and then computes the centroids of those clusters. The distance from these centroids to each vector is computed and the vectors are re-assigned to the cluster with the closest centroid. This process is repeated until the algorithm converges: i.e., when no vectors change cluster membership. Agglomerative clustering is a bottom-up, hierarchical clustering method: each vector starts as its own cluster, and then vectors are successively grouped based on some linkage criterion—e.g., Ward’s method²⁴, in which clusters are merged in a way that minimizes the overall variance within each cluster. (Note that in this analysis we are not working with the full ${\vec{b}}$ vectors, but rather with their norms $\parallel\!\!{\vec{b}}\!\!\parallel$, so all of the calculations described above actually involve scalar values, not multi-element vectors.) We use the R implementation (“changepoint”) of the recursive binary segmentation/likelihood ratio test algorithm²⁵, the scikit-learn implementations of both clustering algorithms²⁶, and the ℓ² norm for all distance computations.

For this model run, all three algorithms yield very similar results, flagging the phase change soon after the introduction of the donor bees at t = 400: agglomerative at t_shift = 427 and both changepoint and k-means at t_shift = 415 (shown superimposed on the norm trace in Fig. 4b). This similarity persists across different model runs: for 50 repetitions of the numerical experiment, the means of the detected t_shift values of the three algorithms were similar: 422.8, 429.0, and 422.2 for k-means, agglomerative, and changepoint, respectively, with standard deviations of 12.9, 27.2, and 12.9. These lags are biologically sensible: since it takes some time for the bees in the arena to first sense the presence of the donors and then cover the distance to them, there will always be a lag between the introduction of the donors and the formation of aggregations. Note that it is difficult to make any assertions about ground truth here—aside from the obvious point that trophallaxis-induced aggregation should not occur before the introduction of the donor bees—without performing more detailed modeling of that sense/move process.

Notably, both k-means and agglomerative algorithms yield clusters that are well delineated in time: that is, nearly all norm values $\parallel\!\!{\vec{b}}(t)\!\!\parallel$ that occur before the phase change t_shift are assigned to the first cluster and nearly all $\parallel\!\!{\vec{b}}(t)\!\!\parallel$ that occur after t_shift are assigned to the second cluster. The delineation is not perfect; rather, there is generally a short span of time where the classification of the $\parallel\!\!{\vec{b}}(t)\!\!\parallel$ values alternate between the two clusters. To formalize this, we define an overlap region [t_left, t_right], where t_left is the first data point that is classified as a member of the second cluster, and t_right is the last data point that is classified as a member of the first cluster. As an example, consider the series of norm values labeled as follows: 0000000000101100010111111111. Here, the boundaries of the overlap region fall at 0000000000 ∣ 101100010 ∣ 111111111 and its width is nine. When an overlap occurs, we take the cluster delineation to fall at the first time step at which no more “mislabeled” vectors occur (i.e., t_shift = t_right). Across the different model runs, the maximum width of the overlap region was five time steps, with an average of 1.75. In view of the fact that time is not included explicitly in the calculations—recall that only the norm values are passed as inputs to the clustering algorithms—a delineation of this crisp is an encouraging result, as it suggests that the topological signature truly captures the salient features of the structure. In the “Applications to experimental data” section, we offer another approach that annotates each normed value with the associated time stamp—i.e., running the clustering algorithms on a set of vectors $[\parallel\!\!{\vec{b}}({t}_{i})\!\!\parallel ,{t}_{i}]$ rather than the scalars $\parallel\!\!{\vec{b}}({t}_{i})\!\!\parallel$—which proves to be useful when the data are not so clean. In the “Discussion” section, we explore the alternative of principal component analysis for dimensionality reduction.

Applications to experimental data

Quantifying the morphology of synthetic data is a useful first test, but the ultimate goal of our work is to understand trophallaxis in real honeybees. To that end, we apply our method to data collected via video from a series of six experiments in a semi-2D arena, shown in Fig. 1a, that measures 36 cm × 36 cm × 2 cm. At the start of each experiment, the arena contains a group of honeybees that had been deprived of food for 24 h. After recording their behavior for several minutes, we introduced multiple donor bees that had retained free access to food until that point. We then continue recording the group motion for about 30 min, as the bees interact and exchange food. Video frames from these experiments are greyscale images of 1400 pixels on a side at a resolution of 60 pixels per centimeter. These data are recorded at 30 frames per second, a rate that far exceeds the temporal resolution necessary to completely capture the motion of the bees, so we downsample to a rate of one frame per second for the following analysis. Since the pixel size in these images dictates the lower bound on the spatial resolution of the morphological analysis, as well as the quantization of the range of that analysis, we use pixels as the fundamental distance unit in the analysis that follows, rather than mks units or body-length scales of the animals. The implications of this are discussed further in the “Discussion” section.

Before we can use TDA to analyze these data, we must first build a point cloud from each frame of these videos. Despite recent improvements^27,28, this is difficult because the bees touch and even occlude one another; see Fig. 5a. This makes it hard for an algorithm to detect the exact positions of individuals in images like these. One can address this by affixing barcodes to each bee, as in ref. ²⁹, or by hand-labeling each image, but those approaches are onerous and expensive, especially when one has 30 + min of 30 fps video. Instead, we use image-segmentation techniques to approximate the positions of the individual bees. To each image, we first apply a Gaussian blur filter with a 7 × 7 pixel kernel to reduce background noise³⁰, then employ local minimum/Otsu thresholding³¹ to distinguish the darker pixels (i.e., bees) from the lighter background. Since the resulting images are still speckled with random false-positive pixels, we use erosion and closure³² to remove them. This produces an image like the one shown in Fig. 5b, with pixels corresponding to bees shown in white and background in black. The next step is to aggregate the contiguous white pixels in the image into groups, with adjacency defined as a shared edge or a corner. We then determine the number of bees in each of these groups by dividing its area (in pixels), by the average area in pixels of a single bee, which we obtain from a separate series of experiments, conducted with the identical experimental setup; see Fig. 6a, b. Finally, we create the point cloud by distributing that number of points randomly inside the boundaries of the group, as shown in Fig. 5c.

Fig. 5: Building a point cloud of bee positions.

a Video frame with an inset showing detailed structure. b Segmented image containing all pixels occupied by bees. c Point cloud. The scale bar in panel a, which corresponds to 5cm, also applies to panel b, c.

Fig. 6: Body size of the honeybees in the experiments.

a Example frame. b Distribution of bee sizes in 100 frames.

The analysis of these point clouds proceeds as described in the previous section, beginning with the construction of a series of Vietoris-Rips complexes from the point cloud at each time t_i. An ϵ value equal to 700 pixels in the experimental video frames—i.e., ≈ 12.7 cm or eight bee body lengths—is adequate to connect all points in the cloud into a single connected component, so we use $[{\epsilon }_{\min },\,{\epsilon }_{\max }]=[1,\,700]$ with Δϵ = 1, all in the units of pixels. As in the analysis of the “Spatiotemporal TDA of honeybee aggregations” section, the number of connected components β₀ for each of these ϵ values become the elements of the column vector for that time point in the CROCKER matrix. An example CROCKER plot for the first 900 s of one of the experimental trials is shown in Fig. 7a. As before, this plot gives clear visual evidence of the phase change in the structure that follows the introduction of the donor bees.

Fig. 7: TDA analysis of the experimental data.

a A CROCKER plot from a laboratory food-exchange experiment like the one pictured in Fig. 1. Computing each column in this plot requires 0.07 s on a Mac 1.7 GHz Quad-Core Intel Core i7 and 16 GB of memory—significantly longer than in Fig. 4 because of the much larger number of ϵ values in the filtration. b The corresponding $\parallel\!\!{\vec{b}}({t}_{i})\!\!\parallel$ time series, with superimposed lines for the results of the change-point detection algorithm (dash-dotted blue line, at t = 475), and the two clustering algorithms: k-means (dotted pink line, at t = 465) and agglomerative (dashed orange line, at t = 447) applied to the time-annotated norm values $[\parallel\!\!{\vec{b}}({t}_{i})\!\!\parallel ,{t}_{i}]$. The solid vertical black line at t = 430 indicates when the fed bees are introduced.

To identify this shift using our methodology, we begin, as before, by reducing each column vector ${\vec{b}}(t)$ of the CROCKER matrix down to a scalar value using the ℓ² norm, then apply the changepoint, k-means, and agglomerative methods to the resulting $\parallel\!\!{\vec{b}}(t)\!\!\parallel$ time series. Since the goal, again, is to identify a single phase change, we set the algorithms up to search for one change-point or two clusters. The change-point algorithm flagged t_shift = 475 in this experiment: i.e., 45 s after the introduction of the donor bees at t = 430. The two clustering algorithms did not produce clean results, however. Unlike in the simulation experiments, they did not find clearly delineated clusters. Rather, the overlap region, where successive points are classified in different phases, spanned more than 90% of the data set: an average width of 845.0 and 830.2 s, respectively, for k-means and agglomerative clustering.

The inability of these algorithms to clearly distinguish the morphological phases in these data—which are quite visible to the eye, both in the videos and in the CROCKER plots—is not surprising, as those plots are far noisier than the ones constructed from the simulation data. In the real world, we often find stray bees (sometimes dead bees) who do not participate in the clustering. As a result, the contrast between the clustering and non-clustering phases in the CROCKER plot is not very drastic, as is clear from the contours in the two phases. In the simulation data, we do not see this effect; rather, the bee-agents move quickly to form clusters and thus the phase change is clear and drastic. To use these clustering algorithms to identify the phase changes in the face of these difficulties, we have to employ a different strategy. Recall that working only on the norms effectively discards the temporal information about each of the values passed to the clustering algorithms. (This is not at issue for the R changepoint algorithm, which treats its input as a time series.) To regain the fact that the data is a time series, we can annotate each norm value with the time step to which it corresponds, yielding tuples of the form $[\parallel\!\!{\vec{b}}({t}_{i})\!\!\parallel ,{t}_{i}]$ where t_i is the time stamp and $\parallel\!\!{\vec{b}}({t}_{i})\!\!\parallel$ is the ℓ² norm of the vector of β₀ values of the associated filtration. This greatly improves the results, reducing the mean widths of the overlap region to 1.667 and 12.167 for k-means and agglomerative clustering, respectively. As shown in Fig. 7b, the agglomerative algorithm, working with the time-augmented data, flagged the phase change 17-time steps after the introduction of the donor bees at t = 430 (i.e., t_shift = 447) while the k-means algorithm signaled that change at t = 465.

An analysis of the t_shift results across multiple trials is somewhat more complicated here than in the model runs of “Spatiotemporal TDA of honeybee aggregations” section because the introduction time of the donor bees is different for each laboratory experiment. To account for this variation, we calculate the number of time steps t_lag between the introduction of the donor bees (t_donor) and the change detected by the clustering algorithms (t_shift) for each experiment and then compute the summary statistics on t_lag = t_shift − t_donor. Across six runs of the experiment, the means and standard deviations of t_lag were [58.33, 115.0] and [87.2, 72.0], respectively, for the k-means and agglomerative clustering algorithms. A primary cause of the large standard deviation in both cases was a single experimental trial (C0133) in which the bees formed a short-lived aggregation before the introduction of the donor bees. The implications of this are discussed at more length in the “Discussion” section. Across all six experimental runs, the mean and standard deviation of the t_lag values produced by the change-point detection algorithm were 71.3 and 15.5. Across all three algorithms and all six experiments, the t_lag values were later for the experimental data than the model runs, suggesting that the delay between the introduction of the donor bees and the formation of aggregations is longer in the experiment than in the simulation. We discuss possible reasons for these observations in the following section.

Discussion

In both simulated and laboratory data, the rich morphological signature produced by persistent homology analysis provided leverage to change-point detection and clustering algorithms for identifying phase changes in the behavior of honeybee aggregations. Bees are a significant application of this TDA-based approach, given the vital role that aggregations play in their biology and behavior. The temporal evolution of the topological signature, as captured in CROCKER matrices, is potentially relevant to the study of other aggregation-related behaviors in bees, including social-network analysis in the context of disease³³, waggle dance communication^34,35, and the aggregation around the queen through chemical communication¹¹. The utility of this methodology encompasses other social insects, such as ants and their trophallaxis behavior³⁶. Given its generality, the applicability of our TDA-based methodology extends beyond biological aggregations: it could be used to identify phase changes in any other dynamically evolving point cloud.

The results of all combinations of the different algorithms and dimensionality reduction techniques described in the previous sections are depicted graphically in Fig. 8. Please see Supplementary Table 1 for the t_lag values for the individual experiments. A comparison of the leftmost two bars and the next two bars (corresponding to the clustering methods with and without time, respectively) brings out the previously noted inability of the two clustering algorithms to identify the phase change in the absence of any information about time. This is not surprising because of the noise in the data, which makes the change in the contours of the CROCKER plot far less abrupt. Explicitly re-introducing time as part of the input to these algorithms made a clear difference in the results. Notably, all of these experimental t_lag values are larger than in the simulations. That is, the bees appeared to form aggregations much more quickly in the model than in the laboratory: 22.8 ± 12.9, 29.0 ± 27.2, and 22.2 ± 12.9 for k-means, agglomerative, and changepoint, respectively—compared to 58.3 ± 87.2, 115.0 ± 72.0, and 71.3 ± 15.5 for the experimental data (augmented with time, in the case of the two clustering algorithms). There are two likely reasons for this. First, the model time scales are not identical to those of the experiments. A calculation of the average speed in the two settings suggests a factor of five difference in those time scales, with the model being faster—which is consistent with the lower t_lag values. Second, the model rules are only an approximation of what the bees really do. Importantly, those rules do not include scenting behaviors, which bees use to communicate information about, for example, the presence of food. This, too, could affect the time scales of the aggregation behavior.

Fig. 8: Survey of results of all phase change detection approaches.

The values of means (black dots) and standard deviations (black whiskers) for t_lag, are measured in seconds after the introduction of the donor bees, across all six experimental data sets. Note that the changepoint algorithm inherently considers the input as a time series, whereas the clustering algorithms do not.

It is perhaps surprising that reducing the dimension of the multi-scale topological signature down to a scalar time series using a method like a norm—which distills each n-element CROCKER vector down into a single number—leaves enough information for algorithms to detect the phase change, but others have observed similar effects³⁷. There are other dimensionality reduction techniques, of course: notably principal component analysis or PCA. To explore this alternative, we repeated the clustering analysis by projecting each ${\vec{b}}({t}_{i})$ onto the first principal component of the overall CROCKER matrix in Fig. 7a, annotated with the associated time stamp: i.e., using the k-means and agglomerative algorithms to seek two clusters in a series of two-vectors of the form $[{c}_{{\vec{b}}({t}_{i})},{t}_{i}]$, where ${c}_{{\vec{b}}({t}_{i})}$ is the projection of ${\vec{b}}({t}_{i})$ onto the first principal component of the entire matrix. The results, respectively, were t_lag = 56.2 ± 89.5 and t_lag = 44.7 ± 140.0. In both cases, the standard deviation was skewed by the experimental trial mentioned above (C0133) in which the bees formed a small, short-lived cluster before the introduction of the donor bees; the agglomerative case was additionally skewed by an early t_shift detection in a second data set (C0128), where a similar but smaller and shorter-lived aggregation formed before t_donor. Repeating the analysis on the ${c}_{{\vec{b}}({t}_{i})}$ values with the changepoint method, we obtained t_lag = 10.5 ± 120.1 across the six experimental trials. Here, too, the C0133 data set was the source of the large σ. A lateral comparison of the norm- and PCA-based results across all three algorithms and all six experiments suggests that the former produces earlier mean t_lag values, but with much larger variability across experiments. (In the C0133 trial, for instance, changepoint flagged a negative t_lag when working with the first principal component and a positive one when given the norm trace.) From both practical and theoretical standpoints, we prefer the norm-based method because it is both simpler and also more temporally precise. Comparing our PCA- vs. norm-based results using the simulated data further supports this conclusion; see Supplementary Table 2 for a description of these results. The principal components computed by PCA incorporate information from the entire CROCKER matrix—explaining the variance of the ${\vec{b}}(t)$ vectors for every time point in the experiment—whereas $\parallel\!\!{\vec{b}}({t}_{i})\!\!\parallel$ is specific to a given time point.

Assessing these results, again, is made difficult by the fact that we do not have ground truth for the phase change. Trophallaxis-induced aggregations should certainly not form before the introduction of the donor bees, but aggregations can form for other reasons in groups of bees: because of generalized attraction between individuals, chemical information exchange³⁸, or even just spatial inhomogeneities that emerge naturally during random walks³⁹. Close examination of the experimental videos shows small, transient aggregations forming and dispersing before t_donor in all six trials. In the two that caused the different algorithms to flag a negative t_lag (C0133 and, to a lesser extent, C0128) these aggregations were simply somewhat larger and longer-lived. The aggregations that formed after the introduction of the donor bees were far larger and longer-lived, as is clear from the contours in the CROCKER plots and the means in Fig. 8. In other words, the TDA-based techniques effectively bring out both the large-scale phase changes and some of the nuances of the behavior.

To study the salience of the different elements of the topological signature for the purposes of clustering the data into these distinct behavioral phases, we use a Chi-square statistical test. To each data point, we assign the label produced by the two clustering algorithms. Then we treat the full ${\vec{b}}$ vector for each time step as a feature vector and determine which of its elements—i.e., the β₀ values for individual ϵ values—is the most highly correlated with those labels. This calculation allows us to reverse-engineer the “most influential” values of the ϵ parameter for each trial. Across all six experiments, the mean of these values was 117.3 ± 27.9 pixels (1.3 ± 0.3 in units of bee body lengths). While it would be inappropriate to impute physical meaning to this result (e.g., mechanisms of honeybee behavior), it does provide a major potential advantage, since it means that one need not build the full filtrations, but rather just a few in that range.

A related matter here is the notion of approximating bees as points. Since this approach effectively neglects their actual spatial extent, it introduces a systematic downward bias in the number of ϵ-connected components for a given ϵ value, since the bee perimeters, which are what really define whether the animals are close, will generally be closer than their centers. A proper study of the effects of this would be a real challenge, requiring the development of novel computer-vision methods (to extract the actual perimeters) and novel TDA techniques that move beyond the fundamental assumption of point-cloud data, perhaps using oriented ellipsoids to define connectivity. However, the results in the previous paragraph—that the “most influential” ϵ value is larger than the length of a bee—suggest that approximating bees as points is not a major issue in our approach.

The analysis scales in the construction of the topological signature are an interesting matter here. Fundamentally, TDA is not about the points, but rather about the spaces between them. In experimental data, the natural metric for those spaces—and thus the appropriate unit for the TDA calculations—is dictated by the measurement apparatus: in our laboratory experiments, the pixel resolution of the video camera. These may, of course, differ in other experimental setups, but there are some standard procedures for setting up the filtration that make this kind of analysis systematic. As mentioned in the “Spatiotemporal TDA of honeybee aggregations” section, it is common to set the lower bound ${\epsilon }_{\min }$ of the range of the scale parameter so that every point is a single component (though obviously not below the resolution of the data). Resolution limits can, of course, create spurious topological effects: if the pixels recorded by the camera are 5mm on a side, for instance, two points that are separated by 1mm will be treated as touching even though they are not. (This is not a shortcoming of TDA, of course, but rather a general issue with data resolution.) The value of ${\epsilon }_{\max }$ is also generally dictated by the data. Since increasing ϵ beyond the value that connects all of the points into a single ϵ-connected component will not add to the information in the topological signature, it makes sense to take ${\epsilon }_{\max }$ such that the entire set is connected, as we do in both our real and synthetic data sets. Between those limits, the number of steps in the filtration dictates the resolution of the topological signature: i.e., how precisely one knows what ϵ value connects the points into a particular number of ϵ-connected components. Since the computational cost of TDA rises with the number of complexes in the filtration, this choice can involve balancing a tradeoff between computational complexity and analysis resolution. This cost is modest in our data sets, which contain tens of points, so we choose the smallest spacing Δϵ of the filtration parameter that is available in the experimental data: one pixel, which is roughly 1/55th of the average body length of the bees in these images. Different data sets, with different numbers of points and/or different spatial resolutions, may require different choices for Δϵ and for $[{\epsilon }_{\min },\,{\epsilon }_{\max }]$. While that will rescale the vertical axis of the associated CROCKER plot, it will not obscure the information that it contains, nor will it affect the performance of our proposed methods.

If food exchanges play a role in the formation of aggregations in a group of honeybees, it is reasonable to explore what happens in longer experiments, when the food has diffused across the group and exchanges are presumably less frequent. Figure 9a shows a CROCKER plot for such an experiment, while Fig. 9b shows the associated norms and clustering results. Interestingly, this experiment reveals an additional change in the morphology towards the end of the experiments—though the three different algorithms flagged that change at quite different times. (Note that the t_lag locations for the first phase change detected by the two clustering algorithms are different than in Fig. 7b because the data set in this experiment contains many more CROCKER vectors, which shifts the geometry of the clusters.) We hypothesize that this third dispersed phase, whose morphology resembles the first one, occurs when the food is distributed evenly across the group and trophallaxis events play less of a role in the behavior of the bees, causing them to gradually break the aggregations and return to a dispersed, random motion pattern, similar to the first phase. However, additional experiments are required to confirm these observations and hypotheses.

Fig. 9: TDA analysis of a longer experiment.

a A CROCKER plot of a longer experiment reveals a second phase change in the morphology, likely at the point where the food is distributed evenly across the group. b Results of the changepoint (dash-dotted blue line), k-means (dotted pink line), and agglomerative (dashed orange line) algorithms applied to the $[\parallel\!\!{\vec{b}}({t}_{i})\!\!\parallel ,{t}_{i}]$ vectors, corroborate this result. Note that an asterisk sign is used to highlight the second change point. As before, the black solid line marks the time at which the donor bees are introduced.

Lastly, our approach has the potential to bring a deeper understanding of collective animal behavior cell aggregations, to insect swarms, bird flocks, and fish schools. Our methodology could be easily extended beyond aggregations as well: e.g., by constructing CROCKER plots from β₁, which counts the number of holes in a point cloud, we could study milling behaviors in honeybee swarms and sheep herds. It can also be applied to higher-dimensional data, such as three-dimensional schools of fish and flocks of birds. Additionally, there is room for enhancement in the methodology itself, such as refining the computer-vision code used to detect the positions of the bees, exploring alternative clustering and change-point detection algorithms, and incorporating other dimensionality reduction techniques. Another important potential affordance of this methodology is model validation via a comparison of topological signatures of simulation and experiment⁹.

In this paper, we have proposed a TDA-based method for detecting phase changes in biological aggregations and demonstrated it on data from honeybees, first in the context of an agent-based model and then using data from laboratory experiments. Persistent homology has been used extensively in the past decade for analyzing the structure of many different kinds of data, ranging from point clouds to images, but identifying phase changes in point-cloud structure has received less attention. CROCKER plots are an effective visual representation of how topological signatures change over time. To leverage that information for the purposes of identifying phase changes, we compress the information in the CROCKER plot into a scalar time series. We used two different dimensionality reduction strategies for this: (i) taking the ℓ² norm of the CROCKER vectors ${\vec{b}}(t)$ at each time point, and (ii) performing PCA on the whole CROCKER matrix and then projecting each ${\vec{b}}(t)$ onto the first principal component. We tested three algorithms on the resulting data: a traditional change-point detection algorithm and two standard clustering algorithms. We demonstrated these approaches on simulated and experimental data sets of honeybee movement, with the goal of detecting the phase change that follows the introduction of donors into a group of deprived bees, as the individuals exchange food and aggregations form.

Our approach differs from existing work in detecting phase changes in evolving point clouds, and the alignment of the results from these approaches indicates their success. All of the different strategies for phase change detection and dimensionality reduction produce roughly similar results, detecting the first phase change within 50–100 s from the time when the donor bees are introduced. Bees are by no means the only application for these strategies; our method can be used to track phase changes in any point cloud, regardless of its provenance, and aid in the understanding of scientific processes that are involved in the dynamics of those data, as well as in validating models of those processes. Overall, we hope that this methodology will help advance our understanding of biological aggregations and their intricate dynamics.

Methods

Methods necessary for the replication of the results are comprehensively described in the “Spatiotemporal TDA of honeybee aggregations” section and the “Applications to experimental data” section.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.