Introduction

Holography emerged as a key concept in high-energy physics, gravity, and quantum information. With the introduction of the anti-de Sitter-conformal field theory (AdS-CFT) correspondence by Maldacena1, holographic duality established a relation between two physical theories, one sitting in the bulk and the other sitting at the boundary of a hyperbolic space2,3. In an effort to understand this AdS-CFT correspondence further, geometrically arranged tensor networks arose as a useful tool, displaying unique entanglement properties4,5,6 This link between geometry and quantum entanglement led to recent efforts seeking an experimental realization of holography7,8,9,10. However, an experimental realization of the proposed tensor networks is challenging.

The hyperbolic pentagon code proposed by ref. 11, also known as HaPPY code, is today’s premier toy model for understanding holographic duality. It is composed of a tensor-network with absolutely maximally entangled states (also known as perfect tensors) as basic building blocks. This model exhibits several desired features such as a uniform bulk and an entanglement entropy constrained by the Ryu-Takayanagi formula12.

Despite recent theoretical investigations into the error-correcting capabilities of holographic codes13,14,15,16,17, experimental implementations have yet to come forward18. In this work we close the gap towards an experimental implementation and bring the stabilizer approach to holography19 to its logical conclusion by formulating it as a graph code. This opens up a path towards investigating AdS-CFT like models experimentally, making their unique partial recovery features accessible for current and upcoming quantum technologies.

Our framework yields a graph state from which we derive the gates necessary to encode, perform logical gates, and decode quantum information. Additionally, it exhibits the essential characteristic of holographic systems, that is the ability to recover a bulk region from its nearby boundary.

While challenging, our toy model can already be implemented with as few as 12 qubits, with experimental requirements that are within reach of current neutral atom platforms20, superconducting qubits21 and trapped ions experiments22.

Recent experimental efforts show the possibility to engineer long-range connectivity in neutral atom systems23,24, trapped ions25,26 and superconducting qubit platforms21. Depending on the platform the long-range interaction between the qubits is realized by coherently transporting the qubits or using a connecting bus.

In contrast to more common methods which require stabilizer measurements to prepare the logical zero state27, our approach reduces this task to a graph state preparation. For the trapped ions set up from28, the graph state fidelity is estimated higher than the fidelity of the state prepared via stabilizer measurements.

Results

Main contribution

We formulate the hyperbolic pentagon code introduced by Pastawski et al.11 in terms of its corresponding stabilizer graph code. This allows to derive the encoding and decoding gates, as well as the partial recovery operations that are required to demonstrate holography experimentally.

Our approach is based on three observations: first, by choosing stabilizer states as building blocks, the hyperbolic pentagon code can be written in stabilizer form19. Second, a stabilizer code which encodes k into n qubits can be represented as a graph code29, that is, a graph state on k + n systems. Third, the number and range of interactions of this graph can be optimized through local Clifford operations, significantly reducing the experimental requirements to prepare the code states.

This procedure allows us to represent the hyperbolic pentagon code as a stabilizer graph code in a manner suitable for experimental implementation (c.f. Fig. 1). In addition, our method also provides the gates necessary to recover parts of the encoded bulk degrees of freedom from their nearby boundary, thus demonstrating holographic features.

Fig. 1: A holographic graph code.
figure 1

A small instance of the hyperbolic pentagon (HaPPY) code11, represented as a graph state or graph code. This representation is obtained from mapping the tensor network to a stabilizer state and then finding an experimentally suitable local Clifford equivalent graph state. The entire construction can be described as a holographic graph code.

Full size image

Following the method described above, we propose an experimental implementation of a small instance of the hyperbolic pentagon code on twelve qubits (c.f. Fig. 1). Through a stabilizer graph code representation, we provide the gates required to encode and decode four bulk qubits into twelve boundary qubits. In addition, we show how to demonstrate holographic features of the logical code states. We list the specific gates needed for a partial decoding operation which recovers two bulk degrees of freedom from their nearby five-qubit boundary.

This places the experimental implementation and certification of holographic systems within reach of current experimental high-connectivity platforms such as Rydberg atoms in optical tweezers, trapped ions, or cavity-coupled qubits. Specifically by using trapped-ion setup from28, we estimate a higher logical zero state fidelity with our method than with currently available ones27. We suggest as first step towards the implementation of the holographic pentagon code, the preparation of the logical zero state. It is noteworthy that our proposal is of a scale that can be compared against numerical simulations. The reader only interested in the experimental implementation can directly jump to A holographic model on 12 qubits.

Holographic code

A holographic code encodes k bulk qubits into n boundary qubits with n > k, such that any bulk region can be recovered from its nearby boundary. The bulk degrees of freedom live in the Hilbert space \({{{{\mathcal{H}}}}}_{{{{\mathcal{B}}}}}\) and host the message, whereas the code space \({{{\mathcal{C}}}}\) is a subspace of the boundary space \({{{{\mathcal{H}}}}}_{\partial {{{\mathcal{B}}}}}\). The encoding of the bulk into the boundary is mathematically defined by a norm-preserving linear map \({T}_{{{{\rm{H}}}}}:{{{{\mathcal{H}}}}}_{{{{\mathcal{B}}}}}\to {{{\mathcal{C}}}}\subset {{{{\mathcal{H}}}}}_{\partial {{{\mathcal{B}}}}}\), i.e., an isometry. The norm-preserving property of isometries can be written as \({T}_{{{{\rm{H}}}}}^{{\dagger} }{T}_{{{{\rm{H}}}}}={{\mathbb{1}}}_{{{{\mathcal{B}}}}}\). For our purposes the corresponding Hilbert spaces are \({{{{\mathcal{H}}}}}_{{{{\mathcal{B}}}}}={({{\mathbb{C}}}^{2})}^{\otimes k}\) and \({{{{\mathcal{H}}}}}_{\partial {{{\mathcal{B}}}}}={({{\mathbb{C}}}^{2})}^{\otimes n}\) but qudit Hilbert spaces are also possible. Then, the isometry can explicitly be written as

$${T}_{{{{\rm{H}}}}}=\mathop{\sum }\limits_{{i}_{1},\ldots ,{i}_{k}=0}^{1}{\vert {H}_{{i}_{1}\ldots {i}_{k}}\rangle }_{\partial {{{\mathcal{B}}}}}{\langle {i}_{1}\ldots {i}_{k}\vert }_{{{{\mathcal{B}}}}}\,,$$
(1)

mapping each computational basis element \(\left\vert {i}_{1}\ldots {i}_{k}\right\rangle\) in \({{{{\mathcal{H}}}}}_{{{{\mathcal{B}}}}}\) to its corresponding logical state \(\vert {H}_{{i}_{1}\ldots {i}_{k}}\rangle\) in \({{{\mathcal{C}}}}\). Given the Pauli gates Xj, Yj, Zj acting on the j-th qubit in \({{{\mathcal{B}}}}\), the isometry TH can be used to find the logical gates, which act on \({{{\mathcal{C}}}}\) in the same way as Pauli gates on \({{{{\mathcal{H}}}}}_{{{{\mathcal{B}}}}}\).

By turning the bra vector acting on \({{{\mathcal{B}}}}\) into a ket, the isometry in Eq. (1) can be represented by an unnormalized quantum state

$$\left\vert H\right\rangle =\mathop{\sum }\limits_{{i}_{1},\ldots ,{i}_{k}=0}^{1}{\left\vert {i}_{1}\ldots {i}_{k}\right\rangle }_{{{{\mathcal{B}}}}}\otimes {\vert {H}_{{i}_{1}\ldots {i}_{k}}\rangle }_{\partial {{{\mathcal{B}}}}}\,,$$
(2)

where we changed the order of the kets (bulk and boundary) for consistency with later sections. Therefore, the holographic code can be described by a state which we term holographic state. From Eq. (2) we see that \(\left\vert H\right\rangle\) is maximally entangled with respect to the bipartition \(\partial {{{\mathcal{B}}}}\) and \({{{\mathcal{B}}}}\), which we denote by \({{{\mathcal{B}}}}| \partial {{{\mathcal{B}}}}\). In reverse, each state of the form given in Eq. (2) induces an isometry. Specifically, absolutely maximally entangled (AME) states, often referred to as perfect tensors when the number of parties is even, are maximally entangled with respect to any bipartition.

An interesting way to construct a holographic code is via a tensor network that uses AME states as building blocks. Here we show how this holographic code can be understood as a graph code11,30. In a tensor network the tensors are connected by lines which correspond to index contractions. While contracting two AME states does not necessarily yield another AME state, the contraction is still an isometry. This fact can be directly seen from the tensor network representation of contracting two AME states. By assembling and contracting the tensors properly, one can construct a state that is maximally entangled across \({{{\mathcal{B}}}}| \partial {{{\mathcal{B}}}}\). Using such a maximally entangled state one can map bulk qubits to boundary qubits. Since we use AME states as building blocks, the isometry is decomposed into further smaller isometries. These smaller isometries allow us to recover bulk qubits from their nearby boundary qubits, making the code holographic.

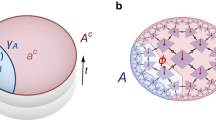
The geometry of the tensor network determines how the decomposition of the isometry is performed and, therefore, which information can be recovered. In this article we consider the hyperbolic pentagon code that contains six-qubit AME states as building blocks11. This AME state was described first as GF(4)-hexacode in a seminal article by Calderbank et al.31 on the connection between classical and quantum stabilizer codes. The state was numerically rediscovered in ref. 32 and brought to graph state form in ref. 33. When the number of parties is even, such states are often referred to as perfect tensors. Figure 2a illustrates the recovery for a specific boundary region: given the boundary qubits on the partition ∂E, it is possible to recover the bulk qubits on E without using the qubits on ∂F.

Fig. 2: Tensor network representation of the hyperbolic pentagon code.
figure 2

The k bulk qubits (in red) are encoded into n boundary qubits (in gold). Each pentagon represents a six-qubit perfect tensor, also known as absolutely maximally entangled (AME) state. The geometry of the assembly makes the holographic state maximally entangled across \({{{\mathcal{B}}}}| \partial {{{\mathcal{B}}}}\). a shows a specific region of the bulk E which can be recovered by reading only the region ∂E of the boundary, where the cut γ is of size ∣γ∣ = 3. b shows a small instance of the code (red) which we propose to prepare experimentally.

Full size image

An important characteristic of holographic codes is that the Ryu-Takayanagi formula holds12. Roughly speaking, given a boundary bipartition ∂E∣∂F and associated bulk regions E∣F, the Ryu-Takayanagi formula states that the entropy of the reduced state on ∂E is proportional to the length of the bulk geodesic that separates E and F, in addition to a bulk entropy term. For the holographic code considered here the formula can be stated as S(∂E) ∝ ∣γ∣ for encoded product states, where ∣γ∣ is the number of contracted indices in the tensor network that cross from the E to F (see Fig. 2b). Linked to this is the ability to perform a partial bulk reconstruction, recovering a part of the bulk from its nearby boundary, a property which can be tested experimentally and will be addressed in Partial decoding circuit.

The construction of holographic codes via tensor networks is well suited to visualize the geometrical aspect of the code. On the other hand the stabilizer formalism is highly efficient in determining encoding and decoding strategies and to obtain the logical states and gates. Hence, we will discuss in the following section the stabilizer formalism in order to apply it to the hyperbolic pentagon code.

Stabilizer states

An m-qubit stabilizer state is characterized by ℓ independent commuting operators gi that form the stabilizer S = 〈g1, …, gℓ〉, with ℓ ≤ m and \(-{\mathbb{1}}\,\notin \,S\). The gi are elements of the m-qubit Pauli group \({{{{\mathcal{P}}}}}^{m}\), which is formed by tensor products of Pauli matrices X, Y, Z and phases { ± 1, ± i}. Note however that the phases of the stabilizer elements are always real. A stabilizer state34,Section 10.5.1 can be written as

$$\varrho =\frac{1}{{2}^{\ell }}\mathop{\sum}\limits_{s\in S}s=\frac{1}{{2}^{\ell }}\mathop{\prod }\limits_{i=1}^{\ell }({\mathbb{1}}+{g}_{i})\,.$$
(3)

The state ϱ is proportional to a projector which acts on a subspace of dimension 2m−ℓ. When ℓ = m the state is pure.

A convenient way to represent a stabilizer state is through its check matrix. This is an ℓ × 2m matrix C = (A∣B) whose rows correspond to the ℓ generators. The matrix A accounts for the X-part and B for the Z-part of the generators: Aij = 1 if gi contains an X at position j, Bij = 1 if gi contains an Z at position j, Aij = Bij = 1 if there is a Y, and Aij = Bij = 0 if there is a \({\mathbb{1}}\). Therefore, the columns carry the information of how the generators act on individual qubits. The generators of two check matrices C1 = (A1∣B1) and C2 = (A2∣B2) commute if and only if

$${A}_{1}{B}_{2}^{\top }-{B}_{1}{A}_{2}^{\top }=0\ .$$
(4)

However, the parity check matrix does not carry all the information about S, since the signs of the generators are not included in C. To keep track of the signs, we add an extra column ω to C such that C = (A∣B∣ω), where ωi = 0 if gi is positive and ωi = 1 if negative.

We recall that elementary row operations modulo 2 on the check matrix leave the stabilizer invariant: the multiplication of generators corresponds to the addition of the respective rows, and the multiplication and relabeling of generators does not affect S. It is important to remark that the multiplication of generators may change signs in ω, e.g., (X ⊗ X)(Z ⊗ Z) = − Y ⊗ Y. How the signs of the generators change is discussed in Section I of the supplementary material.

Graph states constitute a particular case of pure stabilizer states. These are defined by a graph of m vertices connected by edges \(e \in {\rm{E}}\). The generator associated with the vertex i appearing in Eq. (3) is

$${g}_{i}={X}_{i}\mathop{\bigotimes }\limits_{j\in N(i)}{Z}_{j}\,,$$
(5)

where the neighborhood N(i) is the set of vertices j connected to vertex i by an edge. For a graph state, the check matrix reads \(({\mathbb{1}}| \Gamma )\) where Γ is the adjacency matrix, representing the interaction between the qubits, and the phase vector is trivial ω = 0. An equivalent way to define a graph state is via controlled-Z gates CZuv = diag(1, 1, 1, − 1) acting on qubits u and v as

$$\left\vert G\right\rangle =\mathop{\prod}\limits_{(u,v)\in {{{\rm{E}}}}}{{{\mbox{CZ}}}}_{uv}{\left\vert +\right\rangle }^{\otimes n}\,.$$
(6)

Clifford operations are the unitaries that keep the Pauli group invariant under conjugation. An important example is the one-qubit Hadamard gate H which acts as HXH† = Z, HZH† = X and HYH† = − Y. It is known that all qubit stabilizer states are graph states up to local Clifford operations (LC)35,36. Many of the currently known AME states are graph states up to LC, with the notable exception of the recently discovered four-quhex AME state37.

Holographic graph state

Here we aim to find a suitable graph state \(\left\vert {G}^{{{{\rm{opt}}}}}\right\rangle\) for experimental purposes which corresponds to the holographic state \(\left\vert H\right\rangle\) and to the tensor network in Fig. 2a respectively.

An index contraction corresponds to projecting the tensor onto the Bell state and performing a partial trace. This fact can be seen from Eq. (7) by defining an arbitrary state on m qubits and a projector \({P}^{+}=\vert {\phi }^{+}\rangle \langle {\phi }^{+}\vert \otimes {{\mathbb{1}}}^{\otimes m-2}\) with \(\vert {\phi }^{+}\rangle ={\sum \nolimits_{r = 0}^{1}}\vert rr\rangle\) the (unnormalized) Bell state,

$$\begin{array}{ll}{P}^{+}\vert \psi \rangle \,=\,\mathop{\sum }\limits_{r,s=0}^{1}\mathop{\sum }\limits_{{i}_{1},\ldots ,{i}_{m}=0}^{1}\vert rr\rangle \otimes \langle ss| {i}_{1}{i}_{2}\rangle {\psi }_{{i}_{1}\ldots {i}_{m}}\vert {i}_{3}\ldots {i}_{m}\rangle \\ \qquad\quad\,\,=\,\vert {\psi }^{+}\rangle \otimes \mathop{\sum }\limits_{{i}_{3},\ldots ,{i}_{m},s=0}^{1}{\psi }_{ss{i}_{3}\ldots {i}_{m}}\vert {i}_{3}\ldots {i}_{m}\rangle \\ \qquad\quad\,\,=\,\vert {\psi }^{+}\rangle \otimes \vert \chi \rangle \,.\end{array}$$
(7)

Here, \(\vert \chi \rangle\) is the state after the index contraction. Note that the Bell state is a stabilizer state. Therefore, in case of \(\vert \psi \rangle\) being a stabilizer state, so will \(\vert \chi \rangle\) (see ref. 38,Section 2). That can be seen in more details in Section I of the supplementary information where a method to obtain the generators of \(\vert \chi \rangle\) is found.

Our tensor network has the six-qubit AME state as a building block, which can be expressed as a stabilizer state (see its graph representation in Fig. 3). Using this fact the contraction of the hyperbolic pentagon code leads to a stabilizer state \(\left\vert H\right\rangle\).

Fig. 3: Building blocks of the tensor network.
figure 3

Each pentagon tensor with six indices (left) represents a six-qubit AME state, also known as perfect tensor. For our purposes we choose the graph state representation (right).

Full size image

The state \(\left\vert H\right\rangle\) can be transformed into a graph state \(\left\vert G\right\rangle\) through a local Clifford operator V that is composed of a layer of one-qubit Hadamard gates followed by a layer of Z gates,

$$\left\vert G\right\rangle =V\left\vert H\right\rangle \,.$$
(8)

This fact is shown in Section II of the supplementary information. The Hadamard gates transform the check matrix of \(\left\vert H\right\rangle\) to \(({\mathbb{1}}| \Gamma | \omega )\), which is, up to the phase vector ω, the check matrix of a graph state. The Z gates applied set ω = 0. Note that, from the set of local Clifford operations, we only required Hadamard gates to transform \(\left\vert H\right\rangle\) to a graph state, up to the signs of the generators. We emphasize that the contracted qubits are not part of the holographic state but are only needed to construct the encoding.

For a given graph state, there exist many other local unitary equivalent graphs. While not all local unitary equivalent graph states are local Clifford equivalent39,40, it significantly reduces the complexity of the problem by considering only the subset of local Clifford operations. To facilitate the implementation where the boundary qubits are located according to their position in the tensor network, we are interested in preparation protocols that require few interactions of shortest range only. In principle, a graph with such properties can be found by trying all possible mappings to a graph states, by applying local Clifford unitaries brute-force.

A more refined strategy relies on the algorithm from ref. 41: This algorithm allows to generate the set of LC-equivalent graph states on a small number of qubits. The algorithm results in graphs that are nonisomorphic to each other. Thus, exploring all LC-orbit requires to additionally permute the associated vertices followed by checking whether the permuted graph is LC equivalent to the original graph. In practice the following strategy appears useful: one explores the LC-orbit, chooses a graph with a few number of edges, and then further optimizes the range of interactions while making sure of LC equivalence to the original graph. We note however that these steps are computationally intensive: The number of permutations grow super-exponentially. Furthermore, while the exact scaling of the LC algorithm is unknown, the LC orbit might also become super-exponentially large for n ≥ 1241.

For obtaining the graph \(\left\vert {G}^{{{{\rm{opt}}}}}\right\rangle\) (shown in Fig. 1) we have limited ourselves to the following strategy: Exploring the LC-orbit for the graph in Fig. 5b with n = 16 took our desktop computer a few seconds. Then we permuted only the qubits which were part of the building blocks, and checked LC equivalence to the original graph. Here both the LC orbit and equivalence check were carried out with the library from ref. 41. Note that, while the number of its edges is minimal in the LC orbit, the interaction range of the resulting graph may be not. The LC orbit of a n = 22 instance of the holographic code corresponding to six pentagons can still be explored orbit in around 10 min.

However, larger instances seem to require a more heuristic strategy: Instead of exploring the LC-orbit, we then apply heuristically Hadamard gates to \(\left\vert H\right\rangle\) that result in graph states [see Eq. (8)]. Finally, Z gates can always be applied to set ω = 0. Thus they do not play an important role in the optimization. This last strategy seems to work better for symmetric instances of the hyperbolic pentagon code. Surprisingly, it also leads to the improved graph from Fig. 1. Section VIII from the supplementary information shows a larger instance resulting from contracting eleven AME states corresponding to n = 36 qubits.

Holographic graph code

Here we show how the holographic code can be understood as a graph code29,42. From the graph code and its representation as graph state \(\left\vert G\right\rangle\) [see Eq. (8)], we derive the logical basis states [see Eq. (2)]. We emphasize that the results in this section applies for any graph code, including \(\left\vert {G}^{{{{\rm{opt}}}}}\right\rangle\).

We recall that the check matrix of a graph state is described by \(({\mathbb{1}}| \Gamma )\). Since the holographic graph state \(\left\vert G\right\rangle\) is maximally entangled across \({{{\mathcal{B}}}}| \partial {{{\mathcal{B}}}}\), we can write its adjacency matrix as

(9)

where rank(B) = k, as shown in ref. 43,Section II. The n first columns of the X- and Z-part carry the information how the generators act on the boundary qubits and the remaining k columns describe how the generators act on the logical qubits. Here \({\Gamma }_{{{{\mathcal{B}}}}}\), \({\Gamma }_{\partial {{{\mathcal{B}}}}}\) and B represent the interactions within the bulk, within the boundary, and between bulk and boundary qubits respectively. The corresponding edge sets are \({E}_{{{{\mathcal{B}}}}}\), \({E}_{\partial {{{\mathcal{B}}}}}\), \({E}_{\partial {{{\mathcal{B}}}}| {{{\mathcal{B}}}}}\).

Similarly to \(\left\vert H\right\rangle\) from Eq. (2), the graph state \(\left\vert G\right\rangle\) from Eq. (9) can be written as

$$\vert G\rangle =\mathop{\sum }\limits_{{i}_{1},\ldots ,{i}_{k}=0}^{1}{\vert {i}_{1}\ldots {i}_{k}\rangle }_{{{{\mathcal{B}}}}}\otimes {\vert {G}_{{i}_{1}\ldots {i}_{k}}\rangle }_{\partial {{{\mathcal{B}}}}}\,.$$
(10)

The basis elements of the code space \(\vert {G}_{{i}_{1}\ldots {i}_{k}}\rangle\) with i1, …, ik ∈ {0, 1} can be defined as

$$\vert {G}_{{i}_{1}\ldots {i}_{k}}\rangle ={(-1)}^{{\sum }_{(u,v)\in {{{{\rm{E}}}}}_{{{{\mathcal{B}}}}}}{i}_{v}{i}_{u}}\mathop{\prod }\limits_{r=1}^{k}{\bar{X}}_{r}^{{i}_{r}}\vert {G}_{0\ldots 0}\rangle \,,$$
(11)

where \(\left\vert {G}_{0\ldots 0}\right\rangle\) is the logical zero state and \({\{{\bar{X}}_{r}\}}_{r = 1}^{k}\) are the logical \(\bar{X}\) gates,

$$\left\vert {G}_{0\ldots 0}\right\rangle =\mathop{\prod}\limits_{(u,v)\in {{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}}}{{{\mbox{CZ}}}}_{uv}{\left\vert +\right\rangle }^{\otimes n}\,,\,\,\,{\bar{X}}_{r}=\mathop{\bigotimes}\limits_{s=1}^{n}{Z}^{{B}_{rs}}.$$
(12)

Eqs. (11) and (12) are derived in Section III of the supplementary information.

Now, we want to find the remaining logical gates \({\{{\bar{Z}}_{r}\}}_{r = 1}^{k}\) and the generators of the code space \({\{{g}_{r}\}}_{r = 1}^{n-k}\). It is clear that the generators must commute with the logical gates since their action leaves the code space invariant. As they act on \(\partial {{{\mathcal{B}}}}\) only, we consider the boundary qubits of the check matrix Eq. (9) and write it as42,Section 4

(13)

such that rank(B2) = k. Here B is decomposed into two matrices B1, B2 and \({\Gamma }_{\partial {{{\mathcal{B}}}}}\) into three matrices Γ1, Γ2, Γ3.

Performing row operations on Eq. (13) leads to the generators of the code subspace \({{{{\mathcal{C}}}}}_{G}\) and the logical operators \(\bar{Z}\) and \(\bar{X}\). The result is given by

(14)

The proof of this result can be found in Section IV of the supplementary information.

It is important to remark that with the row operations needed to obtain Eq. (14), the phase vector can also change. This will also introduce additional signs [see Section IV of the supplementary information for details] to the logical \(\bar{Z}\) gates and the generators of the code space associated to \(\left\vert G\right\rangle\).

Encoding

We now describe how an arbitrary state is encoded into the holographic code. The layout of Fig. 2 contains k bulk and n boundary qubits. Given the logical gates and the generators for the code subspace [c.f. Eq. (14)], we provide a recipe to encode an arbitrary k-qubit bulk state into the boundary. This recipe is a modification of the encoding method from ref. 42 and can be found in more details in Section V from the supplementary information.

Define the controlled logical gates acting on bulk qubit j in \({{{\mathcal{B}}}}\) as

$$\begin{array}{ll}{{{\rm{C}}}}{\bar{{{{\rm{X}}}}}}_{j}\,=\,\left\vert 0\right\rangle {\left\langle 0\right\vert }_{j}\otimes {\mathbb{1}}+\left\vert 1\right\rangle {\left\langle 1\right\vert }_{j}\otimes \bar{X}\,,\\ {{{\rm{C}}}}{\bar{{{{\rm{Z}}}}}}_{j}\,=\,\left\vert 0\right\rangle {\left\langle 0\right\vert }_{j}\otimes {\mathbb{1}}+\left\vert 1\right\rangle {\left\langle 1\right\vert }_{j}\otimes \bar{Z}\,,\end{array}$$
(15)

with \({\mathbb{1}}\), \(\bar{X}\), and \(\bar{Z}\) acting on the boundary space \(\partial {{{\mathcal{B}}}}\).

A bulk state \(\left\vert {\phi }_{{{{\rm{in}}}}}\right\rangle\) encodes into a boundary state \(\left\vert {\phi }_{{{{\rm{enc}}}}}\right\rangle\) via

$${\left\vert +\right\rangle }_{{{{\mathcal{B}}}}}^{\otimes k}\otimes {\left\vert {\phi }_{{{{\rm{enc}}}}}\right\rangle }_{\partial {{{\mathcal{B}}}}}={U}_{G}\left({\left\vert {\phi }_{{{{\rm{in}}}}}\right\rangle }_{{{{\mathcal{B}}}}}\otimes {\left\vert +\right\rangle }_{\partial {{{\mathcal{B}}}}}^{\otimes n}\right)\,,$$
(16)

where UG = U3U2U1 with

$$\begin{array}{ll}{U}_{1}\,=\,\mathop{\prod}\limits_{(u,v)\in \{{{{{\rm{E}}}}}_{{{{\mathcal{B}}}}},{{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}}\}}{{{\mbox{CZ}}}}_{uv}\,,\quad {U}_{2}=\mathop{\prod }\limits_{j=1}^{k}{{{\rm{C}}}}{\bar{{{{\rm{X}}}}}}_{j}\,,\\ {U}_{3}\,=\,\mathop{\prod }\limits_{j=1}^{k}{{{{\rm{C}}}}\bar{{{{\rm{Z}}}}}}_{j}\left({H}_{{{{\mathcal{B}}}}}^{\otimes k}\otimes {{\mathbb{1}}}_{\partial {{{\mathcal{B}}}}}^{\otimes n}\right)\,.\end{array}$$
(17)

After a successful encoding the bulk degrees of freedom are left in the product state \({\left\vert +\right\rangle }^{\otimes k}\), as illustrated in Fig. 4.

Fig. 4: Encoding scheme.
figure 4

The state \(\left\vert {\phi }_{{{{\rm{in}}}}}\right\rangle\) to be encoded is localized in the bulk, while the boundary qubits are in the product state \({\left\vert +\right\rangle }^{\otimes k}\). After performing the encoding unitary UG the information is mapped to the boundary state \(\left\vert {\phi }_{\rm{enc}}\right\rangle\) and with the bulk in a product state \({\left\vert +\right\rangle }^{\otimes k}\).

Full size image

The unitary UG is decomposed into three unitaries. The gates in U1 take into account the interactions among boundary qubits and bulk qubits separately [\({\Gamma }_{\partial {{{\mathcal{B}}}}}\) and \({\Gamma }_{{{{\mathcal{B}}}}}\) from Eq. (9)]. They prepare the logical zero state and the phases of the logical states respectively. The gates in U2 take into account the interactions between bulk and boundary qubits [B from Eq. (9)], entangling the bulk computational basis with the logical boundary states. Finally, U3 is responsible for disentangling both systems with the information from the bulk transmitted to the boundary. Note that the conditional gates \({{{\rm{C}}}}{\bar{{{{\rm{X}}}}}}_{j}\) and \({{{\rm{C}}}}{\bar{{{{\rm{Z}}}}}}_{j}\) act between the qubit j in \({{{\mathcal{B}}}}\) and the boundary \(\partial {{{\mathcal{B}}}}\), a gate CZuv acts on two qubits u, v that are both in either \({{{\mathcal{B}}}}\) or \(\partial {{{\mathcal{B}}}}\) only.

Since the logical gates are composed by a tensor product of Pauli gates, we can decompose \({{{\rm{C}}}}{\bar{{{{\rm{X}}}}}}_{j}\) and \({{{\rm{C}}}}{\bar{{{{\rm{Z}}}}}}_{j}\) into a product of CXuv and CZuv gates. We can see that with an example. Define a controlled gate composed by Pauli gates:

$$\left\vert 0\right\rangle {\left\langle 0\right\vert }_{1}\otimes {{\mathbb{1}}}_{2345}^{\otimes 4}+\left\vert 1\right\rangle {\left\langle 1\right\vert }_{1}\otimes \left({X}_{2}{Z}_{3}{Y}_{4}{Y}_{5}\right)\,.$$
(18)

One can decompose it as

$${{{\mbox{CZ}}}}_{14}\left({{{\mbox{CX}}}}_{12}{{{\mbox{CX}}}}_{14}{{{\mbox{CX}}}}_{15}\right)\left({{{\mbox{CZ}}}}_{13}{{{\mbox{CZ}}}}_{15}\right)\,.$$
(19)

This decomposition is useful since CX and CZ gates are realizable in many experimental platforms.

Partial decoding

The decoding abilities of the hyperbolic pentagon code are related to its geometry, which is induced by how the AME states are arranged in the tensor network. Their contraction yields the holographic state \(\left\vert H\right\rangle\), which represents an isometry TH that encodes k bulk qubits into n boundary qubits through Eq. (1).

To see how a bulk region can be recovered from its nearby boundary, we partition the bulk into two complementary regions E and F along a cut γ with associated boundary regions ∂E and ∂F, shown in Fig. 2a. To each tensor network leg crossed by the cut γ we associate a qubit. These qubits form the Hilbert space \({{{{\mathcal{H}}}}}_{\gamma }={({{\mathbb{C}}}^{2})}^{\otimes | \gamma | }\). If there exists an isometry from E ∪ γ to ∂E, then the quantum information stored in E can be recovered from ∂E. A way to check whether such isometry exists is through the method of tensor pushing11,Section 5.3. Such a partial isometry can be written as,

$$\begin{array}{ll}{T}_{{{{\rm{h}}}}}\,=\,\mathop{\sum}\limits_{{{{\bf{i}}}}\in {{\mathbb{Z}}}_{2}^{| E| }}\mathop{\sum}\limits_{{{{\bf{j}}}}\in {{\mathbb{Z}}}_{2}^{| \gamma | }}{\vert {h}_{{{{\bf{ij}}}}}\rangle }_{\partial E}{\langle {{{\bf{i}}}}\vert }_{E}\otimes {\langle {{{\bf{j}}}}\vert }_{\gamma }\\\,\quad\,=\,\mathop{\sum}\limits_{{{{\boldsymbol{\ell }}}}\in {{\mathbb{Z}}}_{2}^{| \partial E| }}\mathop{\sum}\limits_{{{{\bf{i}}}}\in {{\mathbb{Z}}}_{2}^{| E| }}\mathop{\sum}\limits_{{{{\bf{j}}}}\in {{\mathbb{Z}}}_{2}^{| \gamma | }}{h}_{{{{\boldsymbol{\ell}} {\bf{ij}}}}}{\vert {{{\boldsymbol{\ell }}}}\rangle }_{\partial E}{\langle {{{\bf{i}}}}\vert }_{E}\otimes {\langle {{{\bf{j}}}}\vert }_{\gamma }\,,\end{array}$$
(20)

where \({\vert {h}_{{{{\bf{ij}}}}}\rangle }_{\partial E}\), forms an orthonormal basis of ∂E.

Given a bulk state that was encoded through the isometry TH, one can apply then a partial isometry \({T}_{{{{\rm{h}}}}}^{{\dagger} }\) on ∂E to recover the bulk region E. This follows from the fact that TH can be decomposed in terms of the elements hℓij from Th as,

$${T}_{{{{\rm{H}}}}}=\mathop{\sum}\limits_{{{{\boldsymbol{\ell}}}}\in {{\mathbb{Z}}}_{2}^{| \partial E| }}\mathop{\sum}\limits_{{{{\bf{i}}}}\in {{\mathbb{Z}}}_{2}^{| E| }}\mathop{\sum}\limits_{{{{\bf{j}}}}\in {{\mathbb{Z}}}_{2}^{| \gamma | }}\left({h}_{{{{\boldsymbol{\ell}} {\bf{ij}}}}}{\left\vert {{{\boldsymbol{\ell}}}}\right\rangle}_{\partial E}{\left\langle {{{\bf{i}}}}\right\vert}_{E}\otimes {R}_{{{{\bf{j}}}}}\right)\,,$$
(21)

where Rj is a tensor mapping from F to ∂F. This decomposition emerges from the tensor network illustrated in Fig. 2a. The isometry Th is constructed by the building blocks geometrically situated in E, which in turn are contracted by ∣γ∣ indices to the rest of the building blocks situated in F.

One sees that TH followed by \({T}_{{{{\rm{h}}}}}^{{\dagger} }\) acts as identity on E i.e.,

$$\begin{array}{ll}&({T}_{h}^{{\dagger} }\otimes {{\mathbb{1}}}_{\partial F}){T}_{{{{\rm{H}}}}}\\ &=\mathop{\sum}\limits_{{{{\bf{i}}}},{{{\bf{{i}}}^{{\prime} }}}\in {{\mathbb{Z}}}_{2}^{| E| }}\mathop{\sum}\limits_{{{{\bf{j}}}},{{{\bf{{j}}}^{{\prime} }}}\in {{\mathbb{Z}}}_{2}^{| \gamma | }}\left(\mathop{\sum}\limits_{{{{\boldsymbol{\ell}}}}\in {{\mathbb{Z}}}_{2}^{| \partial E| }}{h}_{{{{\boldsymbol{\ell}} {\bf{i}}}^{\prime}} {\bf{j}}^{\prime}}^{*}{h}_{{{{\boldsymbol{\ell} {\bf{ij}}}}}}\right)\left\vert {{{\bf{{i}}}^{{\prime} }}}\right\rangle \left\langle {{{\bf{i}}}}\right\vert \otimes {\left\vert {{{\bf{{j}}}^{{\prime} }}}\right\rangle }_{\gamma }\otimes {R}_{{{{\bf{j}}}}}\\ &={{\mathbb{1}}}_{E}\otimes \mathop{\sum}\limits_{{{{\bf{j}}}}\in {{\mathbb{Z}}}_{2}^{| \gamma | }}{\left\vert {{{\bf{j}}}}\right\rangle }_{\gamma }\otimes {R}_{{{{\bf{j}}}}}\,,\end{array}$$
(22)

where we used that \({\sum }_{{{{\boldsymbol{\ell}}}}\in {{\mathbb{Z}}}_{2}^{| \partial E| }}{h}_{{{{\boldsymbol{\ell}} {\bf{{i}^{{\prime} }{j}^{{\prime}}} }}}}^{* }{h}_{{{{\boldsymbol{\ell}} {\bf{ij}}}}}={\delta }_{{{{{\bf{ii}}}}}^{{\prime}}}{\delta }_{{{{\bf{j{j}}}^{{\prime}}}}}\) because the elements \(\vert {h}_{{{{\bf{ij}}}}}\rangle\) form an orthonormal basis. Hence, Th recovers the bulk information of E from its nearby boundary ∂E.

The isometry Th can be represented as a quantum state \(\left\vert h\right\rangle \in {{{{\mathcal{H}}}}}_{E}\otimes {{{{\mathcal{H}}}}}_{\gamma }\otimes {{{{\mathcal{H}}}}}_{\partial E}\). This state is constructed by contracting six-qubit AME states from the regions E and ∂E only and it can be converted to a graph state \(\vert g\rangle\) via local Clifford operations W, such that \(\vert g\rangle =W\vert h\rangle\). Eqs. (16) and (17) allow to obtain the encoding and decoding gates Ug corresponding to \(\vert g\rangle\). As done with the full code \(\left\vert G\right\rangle\), it is practical to optimize this ”partial” graph code \(\vert g\rangle\) with respect to the range and number of gates.

Recall that \(\left\vert G\right\rangle =V\left\vert H\right\rangle\) and \(\vert g\rangle =W\vert h\rangle\), where W, V are composed of local Clifford gates. Then, the decoding gate Ug has to be corrected with corresponding local Clifford gates (see Section VI from the supplementary information),

$${\widetilde{U}}_{{{{\rm{h}}}}}^{{\dagger} }=({V}_{E}^{{\dagger} }{W}_{E}\otimes {{\mathbb{1}}}_{\gamma \partial E})\,{U}_{{{{\rm{g}}}}}^{{\dagger} }\,({{\mathbb{1}}}_{E\gamma }\otimes {W}_{\partial E}{V}_{\partial E}^{{\dagger} })\,,$$
(23)

where VE, V∂E, WE, W∂E contain the local Clifford gates of V and W having support on E and ∂E respectively. Here, \({\tilde{U}}_{{{{\rm{h}}}}}\) is the unitary operator that performs a partial decoding of a boundary state that was encoded via \(\left\vert G\right\rangle\).

Recall that the bulk decomposes as \({{{\mathcal{B}}}}=E\cup F\) and the boundary as \(\partial {{{\mathcal{B}}}}=\partial E\cup \partial F\). Then a state \(\vert {\phi }_{{{{\rm{enc}}}}}\rangle\) that was encoded through \(\left\vert G\right\rangle\),

$${\left\vert +\right\rangle }_{{{{\mathcal{B}}}}}^{\otimes k}\otimes {\left\vert {\phi }_{{{{\rm{enc}}}}}\right\rangle }_{\partial {{{\mathcal{B}}}}}={U}_{{{{\rm{G}}}}}\left({\left\vert {\phi }_{{{{\rm{in}}}}}\right\rangle }_{{{{\mathcal{B}}}}}\otimes {\left\vert +\right\rangle }_{\partial {{{\mathcal{B}}}}}^{\otimes n}\right)\,,$$
(24)

can be partially decoded by \({\tilde{U}}_{{{{\rm{h}}}}}^{{\dagger} }\)

$$\left\vert {\psi }_{{{{\rm{dec}}}}}\right\rangle =\left({\tilde{U}}_{{{{\rm{h}}}}}^{{\dagger} }\otimes {{\mathbb{1}}}_{\partial F}\right)\left({\left\vert +\right\rangle }_{E\gamma }^{\otimes (| E| +| \gamma | )}\otimes {\left\vert {\phi }_{{{{\rm{enc}}}}}\right\rangle }_{\partial {{{\mathcal{B}}}}}\right)\,.$$
(25)

In particular, one can check that for this partially decoded state

$${{{{\rm{tr}}}}}_{F}\left(\vert {\phi }_{{{{\rm{in}}}}}\rangle \langle {\phi }_{{{{\rm{in}}}}}\vert \right)={{{{\rm{tr}}}}}_{\gamma \partial {{{\mathcal{B}}}}}\left(\vert {\psi }_{{{{\rm{dec}}}}}\rangle \langle {\psi }_{{{{\rm{dec}}}}}\vert \right)$$
(26)

holds. Consequently, all quantum information contained in E can be recovered from its nearby boundary ∂E, demonstrating holographic properties. Which other recovery regions are possible is studied in ref. 11,Section 5.3.

A holographic model on 12 qubits

Here we consider a small instance of the holographic code on 12 qubits that exhibits holographic properties and describe the experimental preparation of its logical states, its encoding, as well as the decoding procedures. We also show how to recover a bulk region from its nearby boundary. The methodology relies on the formulation of the hyperbolic pentagon (HaPPY) code11 as a stabilizer graph code derived in the previous sections.

This toy model consists of four connected pentagons, each representing a six-qubit absolutely maximally entangled state (AME), also known as perfect tensor, as illustrated in Fig. 5a. The toy model involves twelve boundary qubits, labeled by 1 to 12, and four bulk degrees of freedom labeled by A, B, C, D, thus requiring 16 qubits in total.

Fig. 5: Four pentagons.
figure 5

Contracting four perfect tensors as shown in (a) leads to a small instance of the holographic code. The contraction is mapped to the graph state from (b). This state can be thought of as an isometry that encodes the bulk qubits (red) into the boundary qubits (golden). Optimizing the range and the number of edges of the graph in Fig. 2b over local Clifford operations leads to the graph in Fig. 1.

Full size image

The building block of the hyperbolic pentagon code is the six-qubit AME state, for which a highly symmetric graph state representation exists (c.f. Fig. 3)33. The contraction of four such states yields the stabilizer state \(\left\vert H\right\rangle\) which carries both information about the code subspace as well as about the encoding. The resulting \(\left\vert H\right\rangle\) can be transformed to a graph state \(\left\vert G\right\rangle\) by the application of a single layer of Hadamard gates and a subsequent layer of Z gates, as shown in Section II from the supplementary information. As \(\left\vert G\right\rangle\) requires many long-ranges CZ gates, it is useful to choose a local Clifford equivalent graph state that requires gates of shortest possible range. Here we choose the state \(\left\vert {G}^{{{{\rm{opt}}}}}\right\rangle\) that is shown in Fig. 1, which can be found by exploring the local Clifford orbit Fig. 6. This graph has no edges that cross the center and is rotational invariant.

Fig. 6: Partial decoding scheme.
figure 6

The encoded state \(\left\vert {\phi }_{{{{\rm{enc}}}}}\right\rangle\) is localized on the boundary, and the bulk qubits on E and the qubits on the cut γ are in the product states \({\left\vert +\right\rangle }^{\otimes | E| }\) and \({\left\vert +\right\rangle }^{\otimes | \gamma | }\) respectively. The partial decoding unitary \({\widetilde{U}}_{{{{\rm{h}}}}}^{{\dagger} }\) transmits the information from the boundary region ∂E to E.

Full size image

From the graph representation of the state \(\left\vert {G}^{{{{\rm{opt}}}}}\right\rangle\) as illustrated in Fig. 1, the logical zero state and the logical \(\bar{X}\) gates are extracted as follows: remove the red vertices (the bulk qubits) and their incident edges one obtain the logical state \(\left\vert {G}_{0000}^{{{{\rm{opt}}}}}\right\rangle\), corresponding to Eq. (12). This logical state is illustrated in Fig. 7. The logical \(\bar{X}\) gates, given through Eq. (12), are determined by the red edges Brs that connect the bulk with the boundary and read

(27)

While the logical \(\bar{X}\) gates can be extracted directly from the graph in Fig. 1, the logical \(\bar{Z}\) operator do not seem to have such simple graphical interpretation. However, they can be found in Eq. (14) and read

$$\begin{array}{cccccccccccccc}&&1&2&3&4&5&6&7&8&9&10&11&12\\ {\bar{Z}}_{{{{\rm{A}}}}}&=&{\mathbb{1}}&Z&Z&Z&X&{\mathbb{1}}&Z&Z&Z&{\mathbb{1}}&{\mathbb{1}}&{\mathbb{1}}\,,\\ {\bar{Z}}_{{{{\rm{B}}}}}&=&{\mathbb{1}}&{\mathbb{1}}&{\mathbb{1}}&{\mathbb{1}}&Z&Z&Z&X&{\mathbb{1}}&Z&Z&Z\,,\\ {\bar{Z}}_{{{{\rm{C}}}}}&=&Z&Z&Z&{\mathbb{1}}&{\mathbb{1}}&{\mathbb{1}}&{\mathbb{1}}&Z&Z&Z&X&{\mathbb{1}}\,,\\ {\bar{Z}}_{{{{\rm{D}}}}}&=&Z&X&{\mathbb{1}}&Z&Z&Z&{\mathbb{1}}&{\mathbb{1}}&{\mathbb{1}}&{\mathbb{1}}&Z&Z\,.\end{array}$$
(28)

Note that the logical gates in Eqs. (27) and (28) preserve the same rotational symmetry as the graph (Fig. 1) from which they are extracted.

Fig. 7: Logical state.
figure 7

The logical state \(\left\vert {G}_{0000}^{{{{\rm{opt}}}}}\right\rangle\) of the 12 qubit hyperbolic pentagon code as derived from the graph state in Fig. 1.

Full size image

The logical operators can be further simplified when multiplied by the code subspace generators. However, we lose the graphical interpretation of the logical \(\bar{X}\) gates. Similarly, the code subspace generators can be optimized by multiplying each other. This can reduce the number of gates used in this section even more (see Section VII from the supplementary information).

Preparing the logical states

We describe how the logical states can be prepared experimentally. Throughout we will use the labeling from Fig. 5a. One starts by preparing the logical zero state \(\left\vert {G}_{0000}^{{{{\rm{opt}}}}}\right\rangle\) that is illustrated in Fig. 7 and whose formula is given by Eq. (12). Prepare \({\left\vert +\right\rangle }^{\otimes 12}\) and apply controlled-Z gates between qubits \(u,v\in {{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}}\),

$$\left\vert {G}_{0000}^{{{{\rm{opt}}}}}\right\rangle =\mathop{\prod}\limits_{(u,v)\in {{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}}}{{{\mbox{CZ}}}}_{uv}{\left\vert +\right\rangle }^{\otimes 12}\,.$$
(29)

Here \({{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}}\) consists of the 28 boundary-to-boundary edges from Fig. 7,

$$\begin{array}{ll}{{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}}\,=\,\left\{(2,1),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),\right.\\ \qquad\quad\,(5,4),(5,7),(5,8),(5,9),(6,7),(6,8),(6,9),\\ \qquad\quad\,(8,7),(8,10),(8,11),(8,12),\\ \qquad\quad\,(9,10),(9,11),(9,12),\\ \qquad\quad\,(11,10),(11,1),(11,2),(11,3),\\ \qquad\quad\,\left.(12,1),(12,2),(12,3)\right\}\,.\end{array}$$
(30)

With the logical zero state prepared, one can now obtain the remaining logical states by applying logical \(\bar{X}\) gates stated in Eq. (12).

Encoding circuit

In the following paragraphs we describe how to encode an arbitrary four-qubit bulk state into twelve boundary qubits. Eqs. (16) and (17) describe the associated encoding procedure for \(\left\vert {G}^{{{{\rm{opt}}}}}\right\rangle\). This yields the encoding unitary HG, which can be decomposed into three parts.

  1. (1)

    Unitary U1 prepares the logical zero state and introduces real phases to the logical states as shown in Eq. (11).

  2. (2)

    Unitary U2 entangles the logical states of the boundary with the computational basis of the bulk.

  3. (3)

    Unitary U3 decouples the bulk from the boundary, yielding the encoded state on the boundary.

Eq. (17) shows the general form of these unitaries, in particular they can be decomposed in terms of CX and CZ gates. For the graph in Fig. 1 they simplify as follows:

$${U}_{1}=\mathop{\prod}\limits_{(u,v)\in {{{{\rm{E}}}}}_{{{{\mathcal{B}}}}},{{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}}}{{{\mbox{CZ}}}}_{uv}=\mathop{\prod}\limits_{(u,v)\in {{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}}}{{{\mbox{CZ}}}}_{uv}\,,$$
(31)

because our graph does not have interaction between bulk qubits \({{{{\rm{E}}}}}_{{{{\mathcal{B}}}}}=0\). The set \({{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}}\) is given in Eq. (30).

Then, U2 can be written as

$${U}_{2}=\mathop{\prod}\limits_{j\in \{{{\rm{A,B,C,D}}}\}}{{{\rm{C}}}}{\bar{{{{\rm{X}}}}}}_{j}=\mathop{\prod}\limits_{(u,v)\in {{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}| {{{\mathcal{B}}}}}}{{{\mbox{CZ}}}}_{uv}\,,$$
(32)

by decomposing the logical gates \({{{\rm{C}}}}\bar{{{{\rm{X}}}}}\) into two-qubit CZ gates according to Eq. (27). Here the set \({{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}| {{{\mathcal{B}}}}}\) is given by

$$\begin{array}{ll}{{{{\rm{E}}}}}_{\partial {{{\mathcal{B}}}}| {{{\mathcal{B}}}}}\,=\,\left\{(\,{{\mbox{A}}},1),({{\mbox{A}}},3),({{\mbox{A}}},4),({{\mbox{A}}},5),({{\mbox{A}}}\,,6)\right.\\ \qquad\qquad(\,{{\mbox{B}}},4),({{\mbox{B}}},6),({{\mbox{B}}},7),({{\mbox{B}}},8),({{\mbox{B}}}\,,9)\\ \qquad\qquad(\,{{\mbox{C}}},7),({{\mbox{C}}},9),({{\mbox{C}}},10),({{\mbox{C}}},11),({{\mbox{C}}}\,,12)\\ \qquad\qquad\left.(\,{{\mbox{D}}},10),({{\mbox{D}}},12),({{\mbox{D}}},1),({{\mbox{D}}},2),({{\mbox{D}}}\,,3)\right\}\,.\end{array}$$
(33)

Finally, U3 reads

$$\begin{array}{ll}{U}_{3}\,=\,\mathop{\prod}\limits_{j\in \{{{\rm{A,B,C,D}}}\}}{{{{\rm{C}}}}\bar{{{{\rm{Z}}}}}}_{j}\left({H}^{\otimes 4}\otimes {{\mathbb{1}}}_{12}\right)\\ \qquad=\,\mathop{\prod}\limits_{j\in \{{{\rm{A,B,C,D}}}\}}\left(\mathop{\prod}\limits_{w\in {W}_{j}}{{{\mbox{CX}}}}_{jw}\mathop{\prod}\limits_{v\in {V}_{j}}{{{\mbox{CZ}}}}_{jv}\right)\left({H}^{\otimes 4}\otimes {{\mathbb{1}}}_{12}\right)\,,\end{array}$$
(34)

where the logical \({{{\rm{C}}}}\bar{{{{\rm{Z}}}}}\) gates are decomposed into CX and CZ gates according to Eq. (28). Here the sets Vj and Wj are given by

$$\begin{array}{ll}{W}_{{{{\rm{A}}}}}=\{5\}\,,\,{V}_{{{{\rm{A}}}}}=\{2,3,4,7,8,9\}\,,\\ {W}_{{{{\rm{B}}}}}=\{8\}\,,\,{V}_{{{{\rm{B}}}}}=\{5,6,7,10,11,12\}\,,\\ {W}_{{{{\rm{C}}}}}=\{11\}\,,\,{V}_{{{{\rm{C}}}}}=\{1,2,3,8,9,10\}\,,\\ {W}_{{{{\rm{D}}}}}=\{2\}\,,\,{V}_{{{{\rm{D}}}}}=\{1,4,5,6,11,12\}\,.\end{array}$$
(35)

Given the three unitaries written as explicit quantum gates, we can proceed to encode a bulk state. Expand a general bulk state as

$$\vert {\phi }_{{{{\rm{in}}}}}\rangle =\mathop{\sum }\limits_{a,b,c,d=0}^{1}{c}_{abcd}\vert abcd\rangle \,,$$
(36)

and prepare the 12 boundary qubits in \({\left\vert +\right\rangle }^{\otimes 12}\). The application of U1 [c.f. Eq. (31)] prepares the logical zero state \(\left\vert {G}_{0000}^{{{{\rm{opt}}}}}\right\rangle\) from Eq. (29) on the boundary,

$${U}_{1}\left({\vert {\phi }_{{{{\rm{in}}}}}\rangle }_{{{{\mathcal{B}}}}}\otimes {\vert +\rangle }_{\partial {{{\mathcal{B}}}}}^{\otimes 12}\right)={\vert {\phi }_{{{{\rm{in}}}}}\rangle }_{{{{\mathcal{B}}}}}\otimes {\vert {G}_{0000}^{{{{\rm{opt}}}}}\rangle }_{\partial {{{\mathcal{B}}}}}\,.$$
(37)

The subsequent application of U2 [c.f. Eq. (32)] entangles the bulk with the boundary,

$$\begin{array}{ll}\vert \psi \rangle \,=\,{U}_{2}\left({\vert {\phi }_{{{{\rm{in}}}}}\rangle }_{{{{\mathcal{B}}}}}\otimes {\vert {G}_{0000}^{{{{\rm{opt}}}}}\rangle }_{\partial {{{\mathcal{B}}}}}\right)\\ \qquad=\,\mathop{\sum }\limits_{a,b,c,d=0}^{1}{c}_{abcd}{\vert abcd\rangle }_{{{{\mathcal{B}}}}}\otimes {\vert {G}_{abcd}^{{{{\rm{opt}}}}}\rangle }_{\partial {{{\mathcal{B}}}}}.\end{array}$$
(38)

Finally, the gate U3 [see Eq. (34)] decouples the bulk from the boundary,

$${U}_{3}\left\vert \psi \right\rangle ={\left\vert +\right\rangle }_{{{{\mathcal{B}}}}}^{\otimes 4}\otimes \mathop{\sum }\limits_{a,b,c,d=0}^{1}{c}_{abcd}{\left\vert {G}_{abcd}^{{{{\rm{opt}}}}}\right\rangle }_{\partial {{{\mathcal{B}}}}}.$$
(39)

The encoded state is then

$$\left\vert {\phi }_{{{{\rm{enc}}}}}\right\rangle =\mathop{\sum }\limits_{a,b,c,d=0}^{1}{c}_{abcd}\left\vert {G}_{abcd}^{{{{\rm{opt}}}}}\right\rangle \,,$$
(40)

with the computational basis \(\left\vert abcd\right\rangle\) mapped to the logical basis \(\left\vert {G}_{abcd}^{{{{\rm{opt}}}}}\right\rangle\).

Partial decoding circuit

The graph code (Fig. 1) gives information on how to perform the encoding. However, it provides little intuition on realizing a partial decoding operation, i.e., recovering a part of the bulk from its nearby boundary. The geometry of the tensor network indicates what partial recovery processes are possible in general as discussed in ref. 11,Section 5.3.

For our toy model, Fig. 8 illustrates how to perform a partial recovery operation for a specific choice of bulk and boundary regions. Consider the specific cut γ from Fig. 8a which separates two regions: ∂E ∪ E and ∂F ∪ F, where E ∪ F are bulk qubits (red) and ∂E ∪ ∂F boundary qubits (gold). Further, we define the black qubits labeled by I, II and III as those associated to each tensor network leg crossed by the cut γ. The cut is placed in such a way that the two contracted AME states in Fig. 8b act as an isometry Th from E ∪ γ to ∂E. As shown in Eq. (22), one can use \({T}_{{{{\rm{h}}}}}^{{\dagger} }\) to recover the bulk qubits from E by only reading the boundary ∂E.

Fig. 8: Decoding scheme for 12 qubit hyperbolic pentagon code.
figure 8

a A cut for which an isometry from the red qubits of E to the golden qubits of ∂E exist. This isometry is illustrated in (b). After that and applying a set of Hadamards, we obtain the graph code (c). This code can be used to recover partially the information of the original encoding in (a).

Full size image

The isometry Th can be represented as a quantum state \(\left\vert h\right\rangle\) obtained by a contraction of two AME states in Fig. 8b. This state \(\left\vert h\right\rangle\) can also be mapped to a graph state by applying local Clifford operations. Again, this graph can be optimized with respect to the number of edges and locality leading to the state \(\left\vert g\right\rangle\) illustrated in Fig. 8c. Section VI from the supplementary information shows how to correct the \({U}_{g}^{{\dagger} }\) for this local Clifford optimized code.

The decoding procedure contains then the following steps:

  1. 1.

    Apply the corresponding local Clifford before \({U}_{g}^{{\dagger} }\).

  2. 2.

    Apply the same procedure as described in Encoding circuit, but for the graph \(\left\vert g\right\rangle\) and in a reverse order since \({U}_{g}^{{\dagger} }={U}_{3}^{{\dagger} }{U}_{2}^{{\dagger} }{U}_{1}^{{\dagger} }\).

  3. 3.

    Apply the corresponding local Clifford after \({U}_{g}^{{\dagger} }\).

For the graphs \(\left\vert {G}^{{{{\rm{opt}}}}}\right\rangle\) and \(\left\vert g\right\rangle\) illustrated in Figs. 1 and 8c respectively, the unitary gate \({U}_{{{{\rm{g}}}}}^{{\dagger} }\) is modified and given by \({\widetilde{U}}_{{{{\rm{h}}}}}^{{\dagger} }={Z}_{B}{U}_{{{{\rm{g}}}}}^{{\dagger} }\) (see the end of Section VI from the supplementary information). First, \({U}_{3}^{{\dagger} }\) can be written as

$$\begin{array}{ll}{U}_{3}^{{\dagger} }\,=\,\left({H}_{E\gamma }^{\otimes 5}\otimes {{\mathbb{1}}}_{\partial {{{\mathcal{B}}}}}^{\otimes 12}\right)\mathop{\prod}\limits_{j\in \{\,{{\rm{A,B}}},{{\rm{I,II,III}}}\,\}}{{{{\rm{C}}}}\bar{{{{\rm{Z}}}}}}_{j}\\ \qquad=\,\left({H}_{E\gamma }^{\otimes 5}\otimes {{\mathbb{1}}}_{\partial {{{\mathcal{B}}}}}^{\otimes 12}\right)\\ \qquad\cdot \,\mathop{\prod}\limits_{j\in \{\,{{\rm{A,B}}},{{\rm{I,II,III}}}\,\}}\left(\mathop{\prod}\limits_{\omega \in {\Omega }_{j}}{{{\mbox{CZ}}}}_{j\omega }\mathop{\prod}\limits_{w\in {W}_{j}}{{{\mbox{CX}}}}_{jw}\mathop{\prod}\limits_{v\in {V}_{j}}{{{\mbox{CZ}}}}_{jv}\right)\,,\end{array}$$
(41)

where the gates \({{{\rm{C}}}}\bar{{{{\rm{Z}}}}}\) decompose into CX and CZ according to

$$\begin{array}{ccccccccccccccc}&&1&2&3&4&5&&&&1&2&3&4&5\\ {\bar{X}}_{{{{\rm{I}}}}}&=&Z&Z&Z&{\mathbb{1}}&{\mathbb{1}}\,,&{\bar{Z}}_{{{{\rm{I}}}}}&=&&Y&Y&X&{\mathbb{1}}&{\mathbb{1}}\,,\\ {\bar{X}}_{{{{\rm{A}}}}}&=&Z&{\mathbb{1}}&Z&Z&{\mathbb{1}}\,,&{\bar{Z}}_{{{{\rm{A}}}}}&=&&Z&X&X&{\mathbb{1}}&{\mathbb{1}}\,,\\ {\bar{X}}_{{{{\rm{III}}}}}&=&{\mathbb{1}}&{\mathbb{1}}&{\mathbb{1}}&{\mathbb{1}}&Z\,,&{\bar{Z}}_{{{{\rm{III}}}}}&=&-&Z&Y&Y&Y&Y\,,\\ {\bar{X}}_{{{{\rm{II}}}}}&=&{\mathbb{1}}&Z&Z&{\mathbb{1}}&{\mathbb{1}}\,,&{\bar{Z}}_{{{{\rm{II}}}}}&=&-&Y&X&Z&Y&Z\,,\\ {\bar{X}}_{{{{\rm{B}}}}}&=&{\mathbb{1}}&Z&Z&Z&Z\,,&{\bar{Z}}_{{{{\rm{B}}}}}&=&-&Z&Y&Y&X&Z\,.\\ \end{array}$$
(42)

In Eq. (41), the sets Ωj, Vj, Wj are given by

$$\begin{array}{lll}{\Omega }_{{{{\rm{I}}}}}=\{2\}\,,&{W}_{{{{\rm{I}}}}}=\{1,2,3\}\,,&{V}_{z}^{{{{\rm{I}}}}}=\{1\}\,,\\ {\Omega }_{{{{\rm{A}}}}}=\varnothing \,,&{W}_{{{{\rm{A}}}}}=\{2,3\}\,,\ \ &{V}_{{{{\rm{A}}}}}=\{1\}\,,\\ {\Omega }_{{{{\rm{III}}}}}=\{2\}\,,&{W}_{{{{\rm{III}}}}}=\{2,3,4,5\}\,,&{V}_{{{{\rm{III}}}}}=\{1,3,4,5\}\,,\\ {\Omega }_{{{{\rm{II}}}}}=\varnothing \,,&{W}_{{{{\rm{II}}}}}=\{1,2,4\}\,,\,&{V}_{{{{\rm{II}}}}}=\{1,3,4,5\}\,,\\ {\Omega }_{{{{\rm{B}}}}}=\varnothing \,,&{W}_{{{{\rm{B}}}}}=\{2,3,4\}\,,\,\,&{V}_{{{{\rm{A}}}}}=\{1,2,3,5\}\,.\end{array}$$
(43)

Note that since the logical \(\bar{Z}\) gates shown in Eq. (42) have extra phases, we need to introduce a new set of gates described by \({V}_{\omega }^{j}\). After expressing the logical \(\bar{Z}\) gates via X and Z and because of Y = iXZ, only ZI and ZIII will have extra phases.

Second, \({U}_{2}^{{\dagger} }\) can be written as

$${U}_{2}^{{\dagger} }=\mathop{\prod}\limits_{j\in \{{{\text{A,B,I,II,III}}}\}}{{{{\rm{C}}}}\bar{{{{\rm{Z}}}}}}_{j}=\mathop{\prod}\limits_{(u,v)\in {{{{\rm{E}}}}}_{\partial E| E\gamma }}{{{\mbox{CZ}}}}_{uv}\,,$$
(44)

by decomposing \({{{\rm{C}}}}\bar{{{{\rm{X}}}}}\) into CZ gates according to Eq. (42). Here the set E∂E∣Eγ is given by

$$\begin{array}{ll}{{{{\rm{E}}}}}_{\partial E| E\gamma }=&\left\{\right.(\,{{\rm{I}}},1),({{\rm{I}}},2),({{\rm{I}}},3),({{\rm{A}}},1),({{\rm{A}}},3),({{\rm{A}}}\,,4),\\ &(\,{{\rm{III}}},5),({{\rm{II}}},2),({{\rm{II}}},3),({{\rm{B}}}\,,2),\\ &(\,{{\rm{B}}},3),({{\rm{B}}},4),({{\rm{B}}}\,,5)\left.\right\}\,.\end{array}$$
(45)

The last unitary \({U}_{1}^{{\dagger} }\) is

$${U}_{1}^{{\dagger} }=\mathop{\prod}\limits_{(u,v)\in {{{{\rm{E}}}}}_{\partial E},{{{{\rm{E}}}}}_{E\gamma }}{{{\mbox{CZ}}}}_{uv}\,,$$
(46)

with the sets EEγ and E∂E given by

$${{{{\rm{E}}}}}_{E\gamma }=\{(\,{{\mbox{II}}},{{\mbox{A}}}),({{\mbox{II}}},{{\mbox{III}}}),({{\mbox{B}}},{{\mbox{A}}}),({{\mbox{B}}},{{\mbox{III}}}),({{\mbox{B}}},{{\mbox{II}}}\,)\}\,,$$
(47)
$${{{{\rm{E}}}}}_{\partial E}=\{(2,1),(4,2),(4,3),(5,4)\}\,.$$
(48)

Starting from the encoded state \(\left\vert {\phi }_{{{{\rm{enc}}}}}\right\rangle\) we introduce five extra qubits, two red from the bulk region E and three black from the cut (Fig. 8b), such that

$$\vert {\psi }_{1}\rangle ={\vert +\rangle }_{E\gamma }^{\otimes 5}\otimes {\vert {\phi }_{{{{\rm{enc}}}}}\rangle }_{\partial {{{\mathcal{B}}}}}\,.$$
(49)

For our graphs \(\left\vert {G}^{{{{\rm{opt}}}}}\right\rangle\) and \(\left\vert g\right\rangle\), we need to apply local Clifford operations after \({U}_{{{{\rm{g}}}}}^{{\dagger} }\) and not before, since \({\widetilde{U}}_{{{{\rm{h}}}}}^{{\dagger} }={Z}_{B}{U}_{{{{\rm{g}}}}}^{{\dagger} }\). Therefore, apply \({U}_{{{{\rm{g}}}}}^{{\dagger} }={U}_{1}^{{\dagger} }{U}_{2}^{{\dagger} }{U}_{3}^{{\dagger} }\) to obtain

$$\left\vert {\psi }_{0}\right\rangle =\left({U}_{1}^{{\dagger} }{U}_{2}^{{\dagger} }{U}_{3}^{{\dagger} }\otimes {{\mathbb{1}}}_{\partial F}\right)\left\vert {\psi }_{1}\right\rangle \,,$$
(50)

and apply ZB to obtain the decoded state,

$$\left\vert {\psi }_{{{{\rm{dec}}}}}\right\rangle ={Z}_{B}\left\vert {\psi }_{0}\right\rangle \,.$$
(51)

The state \(\left\vert {\psi }_{{{{\rm{dec}}}}}\right\rangle\) has the same reduction on E as \(\left\vert {\phi }_{{{{\rm{in}}}}}\right\rangle\) [see Eq. (26)]. Thus the bulk information on E can be recovered from the state \(\left\vert {\psi }_{{{{\rm{dec}}}}}\right\rangle\) by only reading its nearby boundary ∂E. Thus the sequence of unitary gates Eqs. (49)–(50) realizes partial decoding from the encoded state and hence can be used to demonstrate holographic bulk reconstruction.

In summary, we need 12 qubits to prepare a code state, 16 qubits to encode an arbitrary state and 17 qubits to perform partial recovery.

A circuit to perform encoding followed by partial decoding can also be realized with 17 qubits, as shown in Fig. 9. The encoding needs 12 boundary qubits and 4 bulk qubits initialized in a product state and \(\left\vert {\phi }_{{{{\rm{in}}}}}\right\rangle\), respectively. The result of the encoding is a product state in the bulk and an encoded state in the boundary \(\left\vert {\phi }_{{{{\rm{enc}}}}}\right\rangle\). The partial decoding needs 12 qubits from the encoded state in the boundary, 2 qubits (A and B) from the bulk region E that we aim to recover and 3 qubits (I, II and III) from the cut γ. The remaining bulk qubits (C and D) can be recycled to act as qubits on the cut for the partial decoding. Fig. 9 shows how the qubits C and D are reused as I and II. Note that we still need an additional qubit III to perform the partial decoding; we introduce such a qubit in the center.

Fig. 9: Experimental setup with 17 qubits.
figure 9

The bulk qubits A, B, C and D are encoded into the boundary qubits 1, …, 12. After encoding, we reuse the qubits C (now III) and D (now I) and add an extra qubit III to perform the partial decoding. This procedure recovers the bulk degrees of freedom A and B from the boundary given by the qubits 1 to 5.

Full size image

We emphasize that the experimental setup in Fig. 9 describes the case of performing a partial decoding when we have previously performed a general encoding. For performing a partial decoding given a 12-qubit boundary state, we have to add 3 extra qubits as shown in Fig. 8b.

Experimental feasibility

For the implementation of the graph states presented in this work the ability to entangle arbitrary qubits is essential. In many state-of-the-art approaches, the interaction between qubits is local, which constrains the connectivity of the artificial quantum system. Hence, the long-range entangling gates have to be decomposed into local entangling gates which then increases the number of gates necessary to realize an equivalent circuit. However, several platforms are outstanding with their ability to generate non-local connectivity between qubits and hence allow to prepare the entangled graph states. Platforms which provide such connectivity are trapped ions44, Rydberg arrays24, (artificial) atoms coupled to a cavity23,45. In the case of trapped ions, the long-range interaction between two qubits can be achieved by either using the phonon degrees of freedom in an ion crystal46 or a shuttling approach47, i.e., moving the ions next to each other and then entangle them. Similarly, recent experimental progress in Rydberg atom arrays allow for entangling arbitrary pairs of atoms by shuttling the atoms, bringing two atoms next to each other and then entangle them by using the Rydberg blockade mechanism.

In the case of (artificial) atoms coupled to a cavity, the two typical platforms are superconducting qubits coupled to a microwave cavity or Rubidium atoms coupled to a cavity. In superconductor based platforms Josephson junctions are used to form an artificial two level system.45, whereas in the case of atomic systems one frequently uses internal states of the atom23. The range of the interaction can be engineered by exploiting that a photon can travel along a cavity, while the atoms are connected to the cavity. Controlling the coupling between the (artificial) atom and the cavity then allows to engineer long-range interactions.

In principle, all of these three systems trapped ions, Rydberg arrays or (artificial) atoms coupled to a cavity are able to perform arbitrary local unitary operations and one entangling operation between two arbitrary qubits, which is sufficient to perform arbitrary unitary operations between two qubits48. For example, Rydberg atom arrays recently demonstrated the generation of 12-qubit cluster state and a seven-qubit Steane code with related stabilizer measurements24. Similar results were achieved in ion trap setups, where for example a 7 qubit color code49 or a 9-qubit Bacon Shore code state50 were realized.

Reference 51 bench-marked a trapped-ion setup with single-qubit, two-qubit gate and measurement fidelity of 0.99994(3), 0.9981(3) and 0.9972(5), respectively. Using such a setup, we make a simple estimation of the state fidelity. The logical zero state is obtained with a fidelity of 0.947(8) from the gate sequence described in Eq. (29). Other approaches to prepare the logical zero state require non-destructive stabilizer measurements27 and result in a fidelity of 0.88(2). The state fidelity shows a significant advantage in preparing the logical zero state as a graph compared to stabilizer measurements. This estimation is developed with more details in Section VII of the supplementary information.

Related work

Reference 11,Section 5.7–8 already highlighted that the hyperbolic pentagon can be formulated in the stabilizer formalism. The work of ref. 19 then explored more explicitly the stabilizer formulation, taking advantage of index contractions formulated in terms of Bell state projections and obtaining corrections to the Ryu Takanayagi formula for entangled input states. The resulting codes are not yet optimized over local Clifford operations to reduce experimental requirements. Reference52 introduced the concatenation of quantum codes through their graph state representation. This method of concatenation is not directly applicable to a more general tensor network such as the hyperbolic pentagon code, as in this case more general index contractions are required.

Discussion

In this work we provided a systematic method to represent the hyperbolic pentagon (HaPPY) code as a stabilizer graph code. This allows to engineer as of now theoretical models of holography in artificial quantum systems. Interestingly, the formulation as a graph code applies to any code defined through a tensor network with stabilizer states as building blocks. Furthermore, the method is not restricted to qubits, but, with suitable generalizations, also applies to qudits in prime dimensions. This provides us with the tools to engineer other codes in the same manner, e.g., the holographic state30, holographic CSS codes53, and random stabilizer tensor networks5.

Regarding the scalability of our proposal, the local Clifford optimization as performed here is a limiting factor to find experimentally suitable formulations for larger instances of the hyperbolic pentagon code. However, an inspection of the building blocks graphs before the contraction can provide intuition on how the final contracted graph code might look like. Reducing the number of entangling gates and keeping them short range is crucial for current noisy intermediate-scale quantum (NISQ) devices.

Several open questions of interest remain. It is unclear whether the usage of symmetric building blocks always helps in reducing the local Clifford gate complexity for optimizing the number and range of edges. It is also an unknown whether there is an efficient iterative procedure to build a larger holographic graph layer by layer. Finally, it would be interesting to understand the advantages and disadvantages of experimentally implementing the hyperbolic pentagon code in prime dimensions.